算法-线性回归实战

3.1 使用正规方程进行求解

3.1.1 简单线性回归

公式 ：
$y=wx+b$
一元一次方程，在机器学习中一元表示一个特征，b表示截距，y表示目标值。
使用代码进行实现：

导入包

import numpy as np
import matplotlib.pyplot as plt

X = np.linspace(0, 10, num=30).reshape(-1, 1)
# 斜率和截距，随机生成
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)
# 根据一元一次方程计算目标值y并加上‘噪声’，数据有上下波动
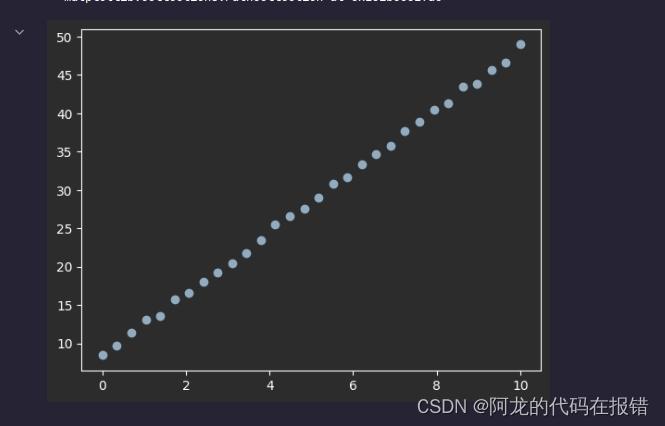
y = X * w + b +np.random.rand(30,1)
plt.scatter(X,y)

# 计算斜率+截距
#系数
X = np.concatenate([X,np.full(shape=[30,1],fill_value=1)],axis=1)
X

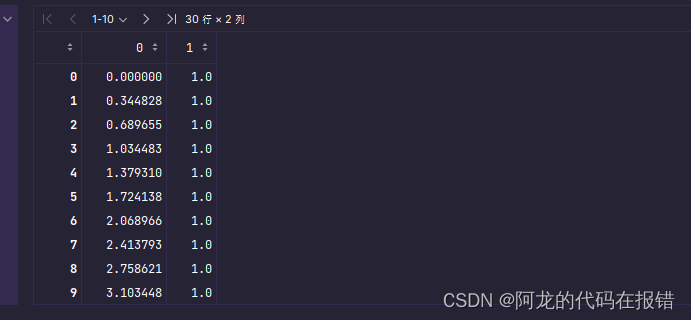
获取系数

coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
w_ = coef_[0,0]
b_ = coef_[1,0]
print('正规方程算法计算，系数',w_,b_)

真实的系数

print('原始的数据斜率、截距',w,b)

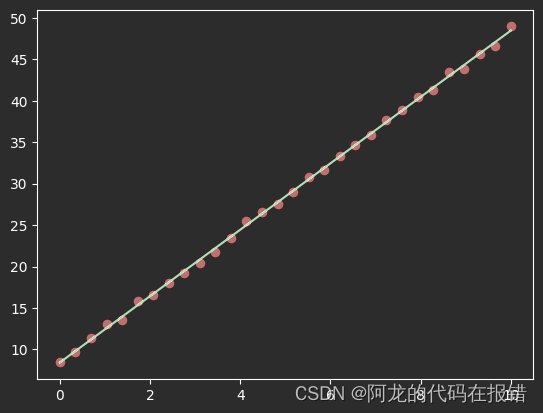
绘制图形

plt.scatter(X[:,0],y,color='red')
plt.plot(X[:,0],X[:,0] * w_ + b_,color='green')

3.1.2 多元的线性回归

公式：
$y=w_1{x}_1+w_2{x}_2+b$
导入包

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D  # 绘制三维图像·

# 转化为矩阵
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))
# 斜率和截距，都是随机生成的
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)
# 根据二元一次方程计算目标值y 并且加上“噪声”，让数据上下波动
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
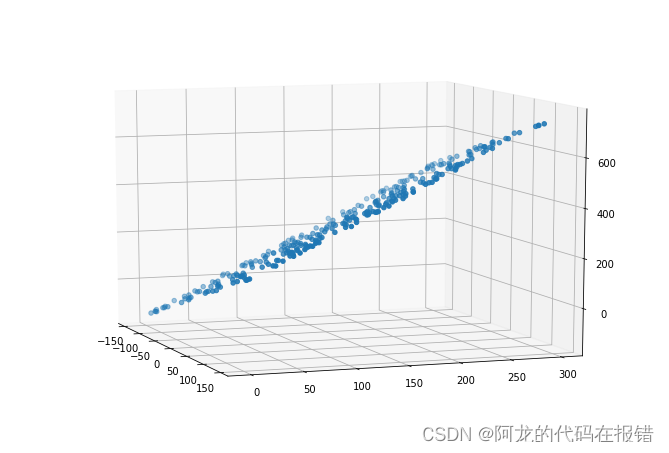
ax.scatter(x1,x2,y) #三维散点图
ax.view_init(elev=10,azim=-20) # 调整视角

X = np.concatenate([x1,x2,np.full(shape=(300,1),fill_value=1)],axis = 1)
X

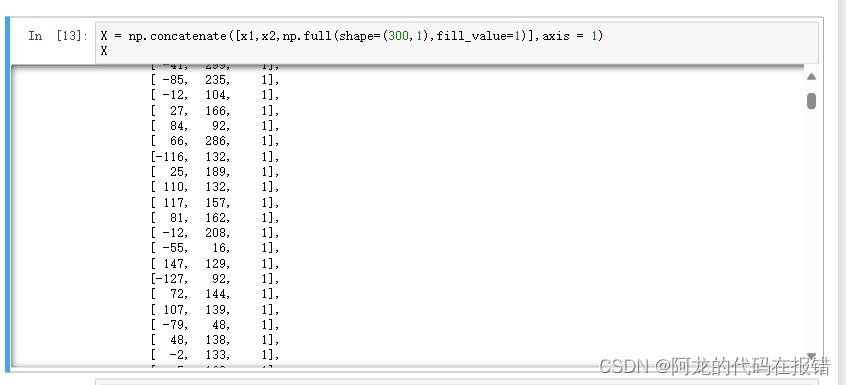
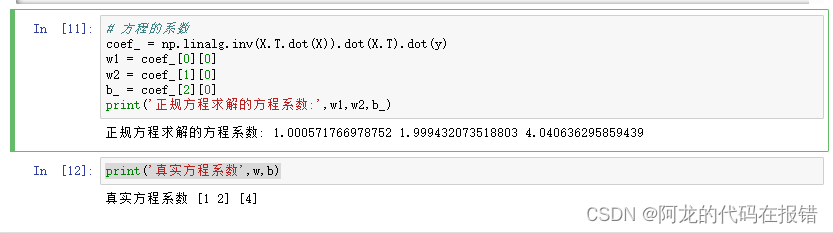
# 方程的系数 
coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
w1 = coef_[0][0]
w2 = coef_[1][0]
b_ = coef_[2][0]
print('正规方程求解的方程系数:',w1,w2,b_)

print('真实方程系数',w,b)

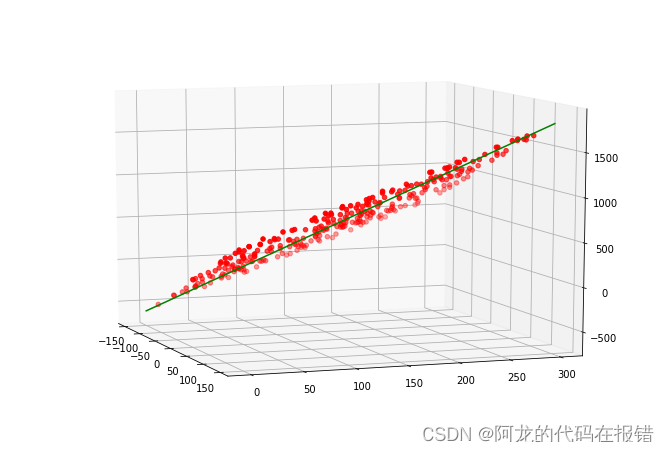
绘制拟合线段

fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y,color='red') #三维散点图
ax.view_init(elev=10,azim=-20) # 调整视角
# 特征1：x1
x = np.linspace(-150,150,num=500)
y = np.linspace(0,300,num = 500)
z = x *w1_+ y*w2_ +b
ax.plot(x,y,z,color='green')