算法-常用排序算法

本博客将讲述常见的几种排序算法

在日常码代码时，常常会用到排序，排序算法又有很多，每种排序都会有自己的特点和适用情况，

我在这将总结几种排序算法，废话少说，开始！

冒泡排序（bubble sort）

冒泡排序，因像水泡一样一个接一个地冒出水面（排序），而得名。

冒泡排序的思想是每次将最大的一次一次运到最右边，然后将最右边这个确定下来。再来确定第二大的，再确定第三大的.....

对于数组a[]，具体的来说，每次确定操作就是从左往右扫描，如果a[i]>a[i+1]，我们就执行swap(a[i],a[ i+1])将两项交换，然后再往右检查，这样可以找出最大的并将其丢到最右边。

第一次确定操作是将a[1]~a[n]中最大的放到a[n];

第二次确定操作是将a[1]~a[n-1]中最大的放到a[n-1]。

依此类推（类似地，如果你想先把最小的放到左边也是可以的)，时间复杂度为O(n^2)。由于排序过程中，数字像冒泡泡一样从左往右换过去，故名冒泡排序。可以多观看下面动图复制理解。

代码如下：

注意：外循环不需要n次，最后两个比一次即可。

内循环需要n-i次，其余i次前面循环已经比较不需要再进行比较

 for(int i=1;i<n;++i)//注意是n，比较不需要比完，最后两个比一次即可
  {
    for(int j=1;j<=n-i;++j)//i的前面比较情况就已经将最大或最小的选出，因此不需要到n次
    {
      if(a[j]>a[j+1])
        swap(a[j],a[j+1]);
    }
  }

选择排序（select sort）

选择排序的思想和冒泡排序类似，是每次找出最大的然后直接放到右边对应位置，然后将最右边这个确定下来（而不是一个一个地交换过去)。

再来确定第二大的，再确定第三大的....

对于数组a[]，具体的来说，每次确定操作（假设当前要确定的是i位置)就是从左向右扫描，计算出

最大元素的下标max_id，最后执行一次swap(a[max_id],a[i])将两项交换即可。

第一次确定操作是将a[1]~a[n]中最大的放到a[n];

第二次确定操作是将a[1]~a[n-1]中最大的放到a[n-1]。

类推（类似地，如果你想先把最小的放到左边也是可以的)，时间复杂度为O(n^2)。

注意比较范围是所有元素，这点与冒泡排序不同。因为要挑选而不是比较。

//i表示当前位置
for (int i = n; i >= 1; --i)
{
	int max_id = 1;//初始化为1
	//j从左向右扫求出max_id
	for (int j = 1; j <= i; ++j)
	{
		if (a[j] > a[max_id])
			max_id = j;
	}
	swap(a[max_id], a[i]);
}

插入排序（insert sort）

插入排序是一种简单直观的排序算法，其基本思想是将待排序的元素逐个插入到已排序序列的合适

位置中，使得已排序序列逐渐扩大，从而逐步构建有序序列，最终得到完全有序的序列。

它类似于打扑克牌时的排序方式，将一张张牌插入到已经有序的手牌中。时间复杂度O(n^2)

插入排序一般用双重循环来实现。

初始时，我们认为长度为1的数组a[1]是有序的(显然)，然后将a[2]插入到合适的位置，使得a[1~2]有序,然后将a[3]插入，使得a[1~3]有序....直至a[1 ~n]有序。

for (int i = 2; i <= n; ++i)
{
	//此时[1，i-1]已经为有序的数组
	int val = a[i], j;
	//将val与a[j-1]比较
	//如果val<a[j-1]就将a[j-1]往后移移动一格
	//给val留出位置
	for (j = 1; j > 1 && val < a[j - 1]; --j)
	{
		a[j] = a[j - 1];
	}
	//当循环跳出时，j=1或valL>=a[j]，且此时a[j]已经向后移动一位
	//此时的j为给val腾出的位置
	a[j] = val;
}

快速排序(quick sort)

快速排序是一种基于分治法的排序方法，原理是将一个数组分成两个子数组，其中一个子数组的所

有元素都小于另一个子数组的元素，然后递归地对这两个子数组进行排序。

快速排序的思想是通过不断地将数组分成两个子数组，递归地对子数组进行排序，最终得到一个有

序的数组。这个过程通过选择合适的基准和分区操作来实现。

快速排序拥有更好的时间复杂度O(nlogn)，且不需要额外空间。

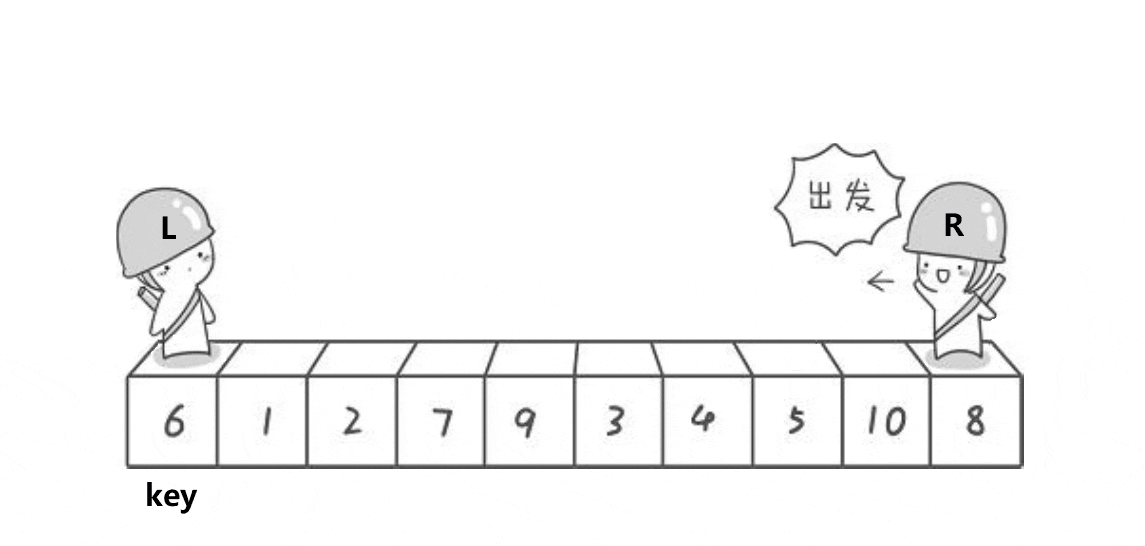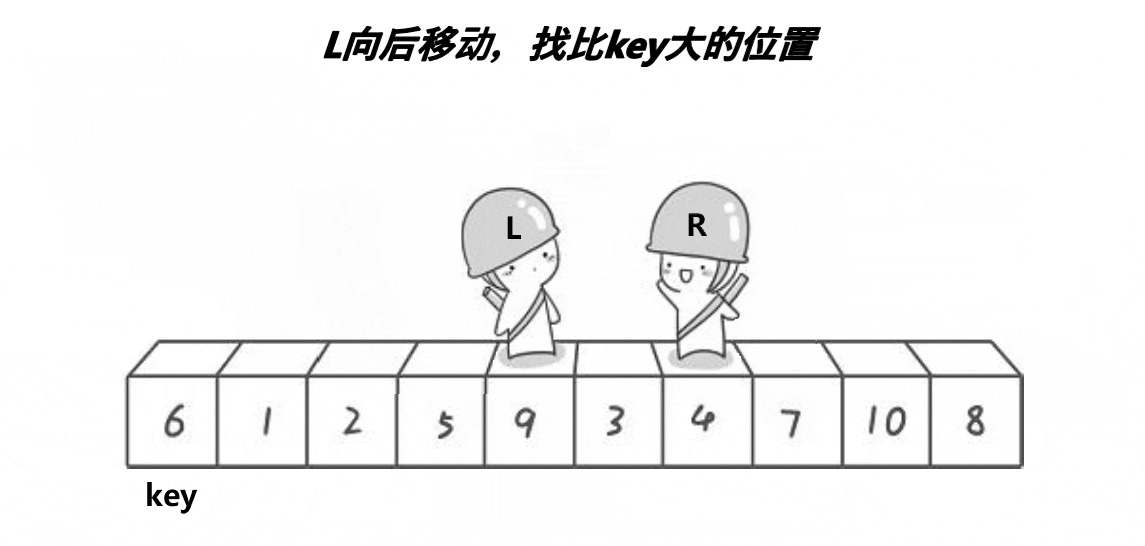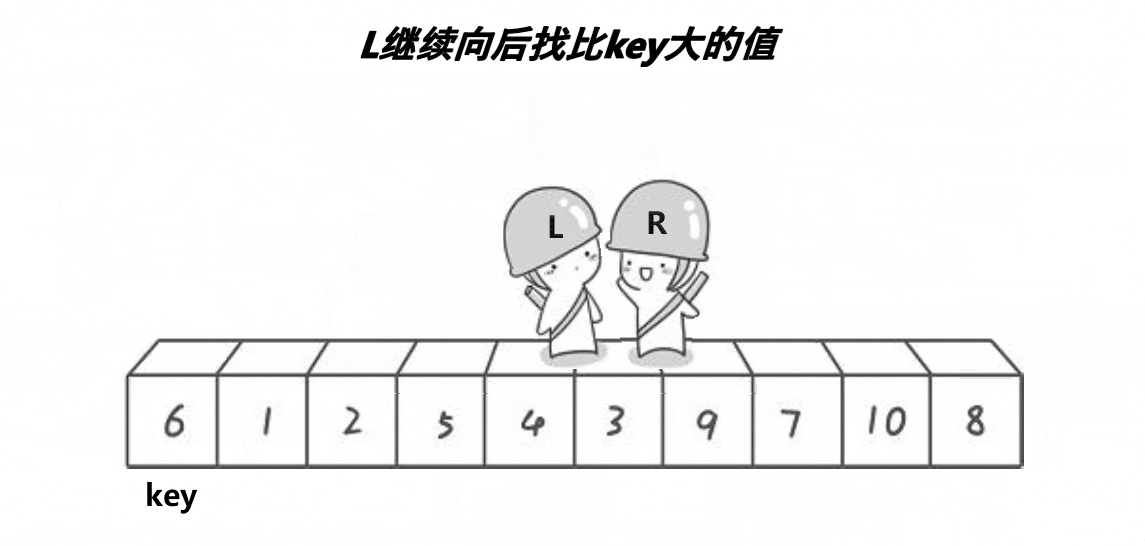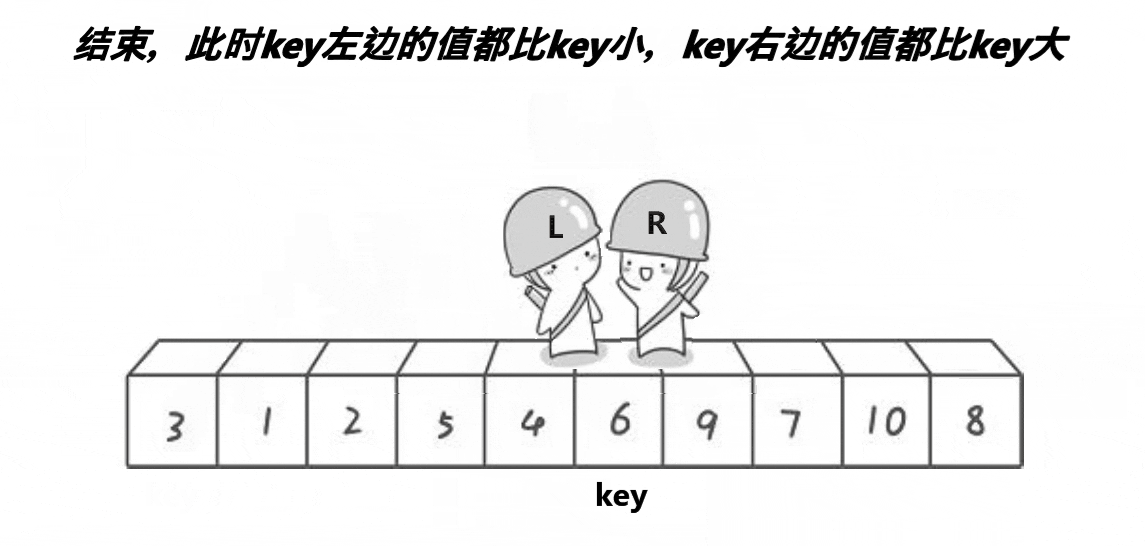
下列是快速排序的代码

代码注解：快速排序的递归主体QuickSort()，传入参数为要排序的数组和区间的左右端点。
Partition函数会将数组a[1]~ a[r]这个区间中某个基准数字放到正确的位置并将这个位置返回。
在确定了mid的位置之后，可以保证a[1]~ a[mid - 1]都<a[mid]< a[mid+1]~a[r]，于是只需要将左右两边分别向下递归地排序即可。

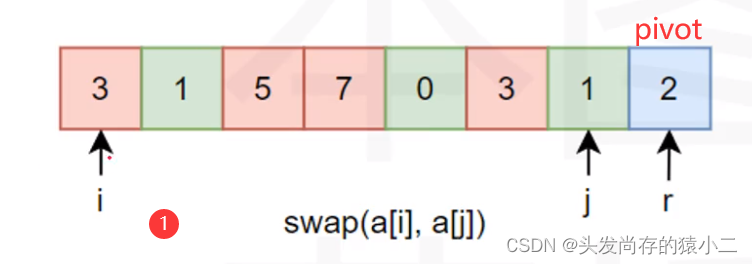
Parition函数(分区函数)，用于将比pivot小的放到左边，大的放到右边，最后返回pivot所处的位置。

int Partition(int a[], int l, int r)//分区函数
{
	//设a[r]为基准，这一次partition会将a[r]放在正确位置上
	int pivot = a[r];
	//设这两个下标i,j分别从l,r开始向中间走
	int i = 1, j = r;
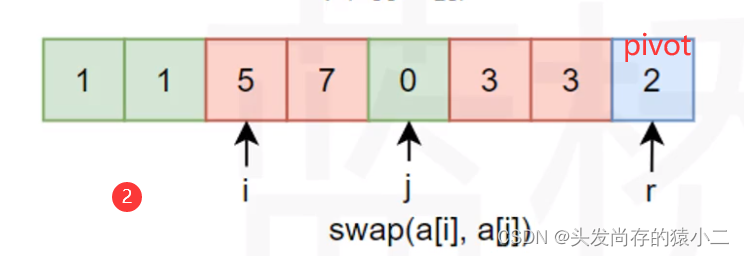
	while (i < j)
	{
		while (i < j && a[i] <= pivot)i++;
		//从上面循环出来后有i>=j或a[i]>pivot(说明找到了需要交换的位置)

		while (i < j && a[j] >= pivot)j--;
		//从上面循环出来后有i>=j或a[j]<pivot(说明找到了需要交换的位置)

		//如果i<j说明存在a[j]<pivot,否则就是a[r]<=pivot，a[i]>=pivot
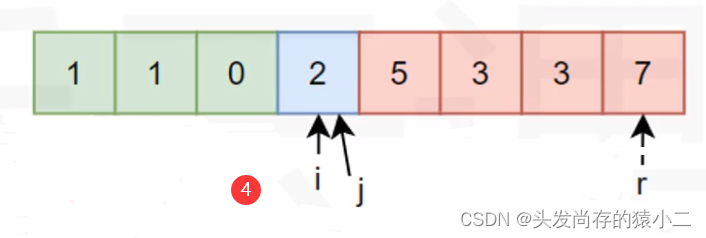
		if (i < j) swap(a[i], a[j]);
		else swap)(a[i], a[r]);
	}
	return 1;
}
void QuickSort(int a[], int l, int r)
{
	if (l < r)//合法区间
	{
		int mid = Partition(a, l, r);
		QuickSort(a, l, mid - 1);
		QuickSort(a, mid+1, r);

	}
}

归并排序(merge sort)

归并排序和快速排序类似，也是一种基于分治法的排序方法。

原理是将一个数组分成两个子数组，将子数组向下递归的排序后（当数组中仅有一个元素值无需再

排序了，直接返回)，得到两个有序数组，然后进行O(n)的合并，最终合并成有序的原数组。

快速排序拥有较好的时间复杂度O(nlogn)，但需要额外的空间用于合并数组。

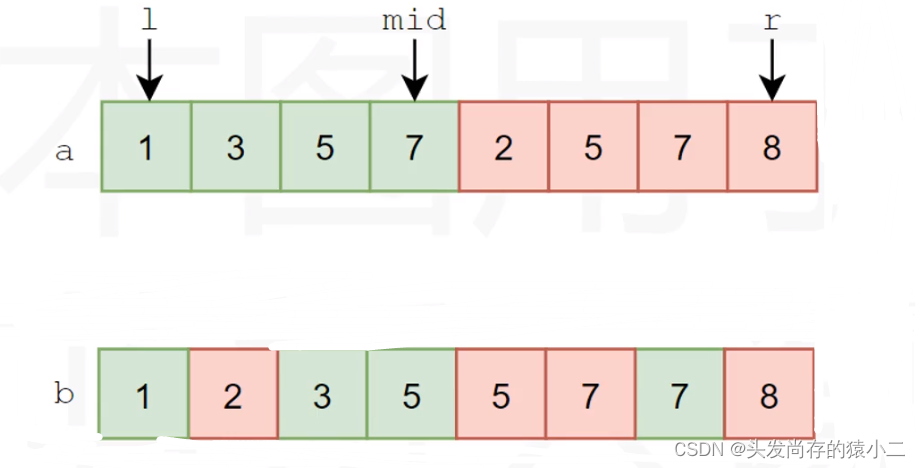
代码如下

void MergeSort(int a[], int l, int r)
{
	if (l == r)return;//区间为1，直接返回

	int mid = (l + r)/2;//注意这里会默认向下取整
	MergeSort(a, l, mid);
	MergeSort(a, mid+1, r);
	//排序完成后a[l,mid]和a[mid+1,r]都是分别有序的

	//将a[l,r]两部分一个个地放入到b[l,r]
	int pl = l, pr = mid + 1, pb = l;//pl左半边下标，pr右半边下标,pb新数组下标
	while (pl < mid || pr <= r)
	{
		if (pl > mid)
		{
			//左半边已经放完
			b[pb++] = a[pl++];
		}
		else if (pr > r)
		{
			//右面已经放完
			b[pb++] = a[pl++];
		}
		else
		{
			//两面都还有元素，取小的放到b中
			if (a[pl] < a[pr])
				b[pb++] = a[pl++];
			else
				b[pb++] = a[pr++];
		}
	}
	//完成后复制回去
	for (int i = l; i <= r; ++i)
		a[i] = b[i];
}

注明：本博客图片来源自网络，如有侵权，联系本人删除，谢谢！

少年没有乌托邦，心向远方自明朗！

如果这个博客对你有帮助，给博主一个免费的点赞就是最大的帮助❤
欢迎各位点赞，收藏和关注哦❤
如果有疑问或有不同见解，欢迎在评论区留言❤
后续会继续更新大连理工大学相关课程和有关算法的内容和代码
点赞加关注，学习不迷路，好，本次的学习就到这里啦！！！

我们下次再见喽！