算法-C++_回文串

目录

 回文子串

最长回文子串

 分割回文串 IV

 分割回文串 II

 最长回文子序列

 让字符串成为回文串的最少插入次数

 回文子串

647. 回文子串

思路，i  j表示改范围内是否为回文串，

②倒着遍历是为了取出dp[i + 1][j - 1]

③i j 只有一对，不会重复，其实就是遍历

参考代码

class Solution {
public:
    int countSubstrings(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n));
        int ret = 0;
        for(int i = n - 1; i >= 0; i--)
        {
            // dp[i][i] = true;
            // for(int j = i + 1; j < n; j++)
            // {
            //     if(s[i] == s[j])
            //         dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;
            //     if(dp[i][j]) ret++;//判断每一次
            // }
            for(int j = i; j < n; j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;//只有最后一层会越界，但是
                if(dp[i][j])
                    ret++;
            }

        }
        // return ret + n;
        return ret;
    }
};

最长回文子串

5. 最长回文子串

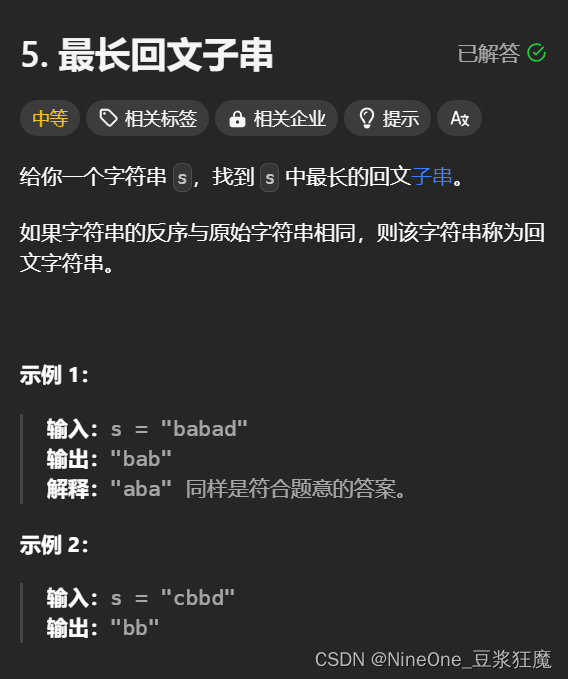
思路区间[i,  j] 是true时候再判断

参考代码

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        int maxlen = 1, begin = 0;
        for(int i = n - 1; i >= 0; i--)
        {
            dp[i][i] = true;
            for(int j = i + 1; j < n; j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;
                if(dp[i][j] && j - i + 1 > maxlen)
                    maxlen = j - i + 1, begin = i;
            }
        }
        return s.substr(begin, maxlen);
    }
};

 分割回文串 IV

1745. 分割回文串 IV

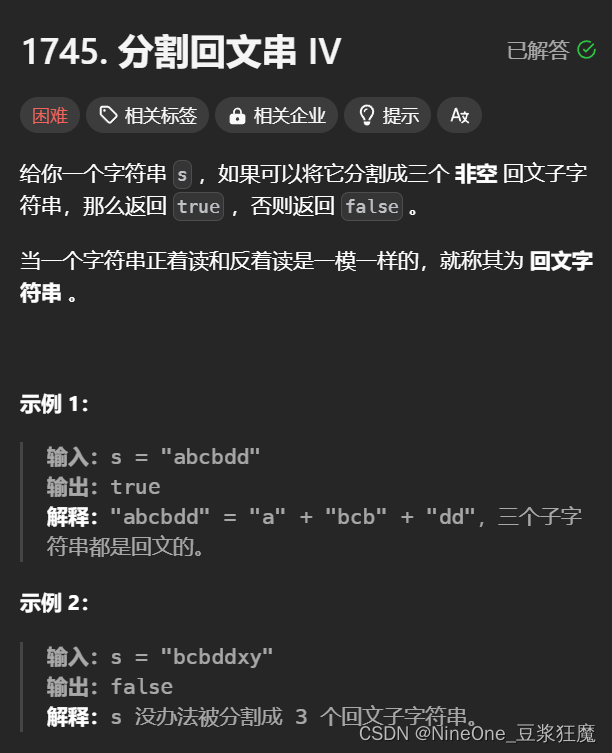
用区间[i, j]即可分成三段 ，只要i j 不同，三段必不相同

参考代码

class Solution {
public:
    bool checkPartitioning(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n));
        for(int i = n - 1; i >= 0; i--)
            for(int j = i; j < n; j++)
                if(s[i] == s[j])
                    dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;
        for(int i = 1; i <= n - 2; i++)
            for(int j = i; j <= n - 2; j++)
                if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])
                    return true;
        return false;
    }
};

 分割回文串 II

132. 分割回文串 II

刚开始打算用dp[i, j]区间内需要的次数 ，发现逻辑就不对，以左右单个字符拎出来，在min剩下的，最小分割的位置很可能在中间某个位置；所以打算重新遍历数组，和139. 单词拆分的思路很像，[0, i] 区间存放的就是最小分割次数

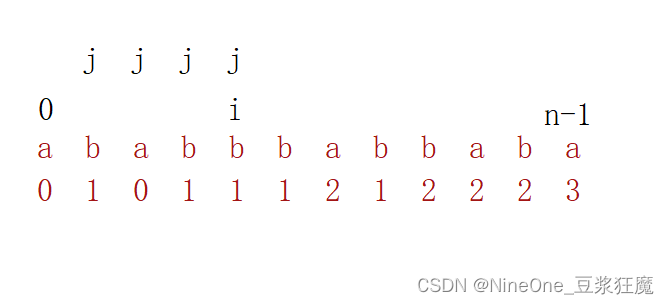
参考代码

class Solution {
public:
    int minCut(string s) {
        // int n = s.size();
        // vector<vector<int>> dp(n, vector<int>(n));
        // for(int i = n - 1; i >= 0; i--)
        // {
        //     for(int j = i + 1; j < n; j++)
        //     {
        //         if(s[i] == s[j])
        //             dp[i][j] = dp[i + 1][j - 1];
        //         else
        //             dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
        //     }
        // }
        // return dp[0][n - 1];
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n));
        for(int i = n - 1; i >= 0; i--)
            for(int j = i; j < n; j++)
                if(s[i] == s[j]) dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;
        vector<int> times(n, INT_MAX);
        times[0] = 0;
        for(int i = 1; i < n; i++)
        {
            if(dp[0][i]) times[i] = 0;
            else
                for(int j = 1; j <= i; j++)
                    if(dp[j][i])
                        times[i] = min(times[i], times[j - 1] + 1);
        }
        return times[n - 1];
    }
};

 最长回文子序列

516. 最长回文子序列

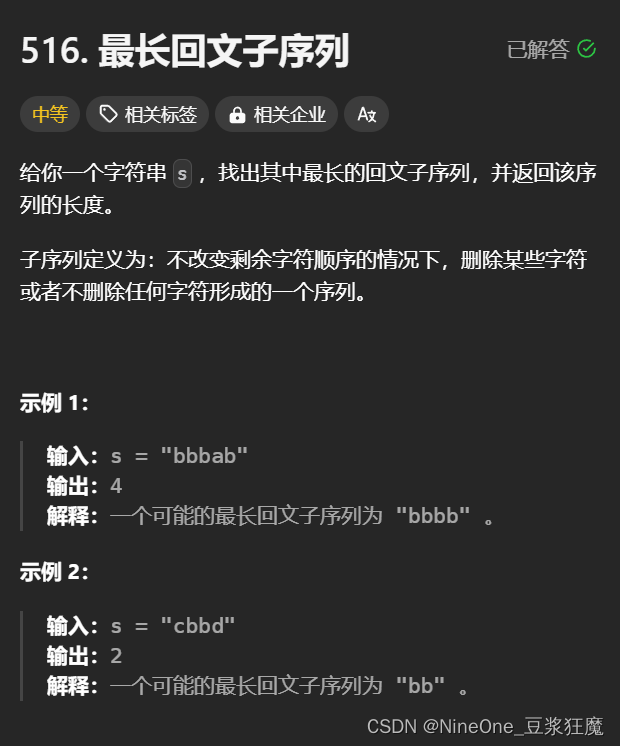
 因为[i ,j] 表示的是区间内的最长回文子序列，这里我不怎么能直接理解，这里的j每次往后走，应该是去尝试匹配s[i]，那么有人会说s[i] 可能和[i + 1, j - 1] 区间内有匹配了，那么用s[j]去匹配，不就少了一个吗？其实不然，这时候中间不管是否和s[i]相同,【 s[i] ,中间字符，s[j] 】就是一个回文子序列，这样是最大的；如果不相等，因为说了，状态表示的是区间内的最长回文子序列，这时候去已经有的区间里面找最长的已知区间就是[i + 1, j] 和 [i , j + 1]，那为什么不去[i, j] 里找，因为没有啊，这时候，dp[i][j]是左值呀

参考代码

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 1));
        for(int i = n - 1; i >= 0; i--)
        {
            for(int j = i + 1; j < n; j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] + 2 : j - i + 1;
                else
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
        return dp[0][n - 1];
    }
};

 让字符串成为回文串的最少插入次数

 1312. 让字符串成为回文串的最少插入次数

 dp表示的是区间[i,  j] 内需要添加的最小次数，同样的道理，如果不相等就是去消除s[i] 或者s[j]，消除伴随着 +1，也就是dp[i][j] = min(dp[i][j - 1], dp[i + 1][j]) + 1,你可能会感觉不对，  有可能是min(dp[i][j - 2], dp[i + 2][j])那么随之后面就要+2，但是这个时候可能s[i] 和s[j - 1]是相等的啊，那么就多添加了一个字符

参考代码

class Solution {
public:
    int minInsertions(string s) {
    int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        for(int i = n - 1; i >= 0; i--)
        {
            for(int j = i + 1; j < n; j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = dp[i + 1][j - 1];
                else
                    dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
            }
        }
        return dp[0][n - 1];
    }
};

总结:通过区间[i,  j]来表示每个区间是否为回文串 ，是的话在进行怎样怎样的操作

我的错误发生： i总是写错i++, 注意力不集中