python-Tensorflow2.0笔记 - 均方差MSE和交叉熵CROSS ENTROPHY作为损失函数

        本笔记主要记录使用MSE和交叉熵作为loss function时的梯度计算方法。

import tensorflow as tf
import numpy as np

tf.__version__


#softmax函数使用
#参考资料：https://blog.csdn.net/u013230189/article/details/82835717
#简单例子：
#假设输出的LOGITS SCORE为：
#2.0
#1.0
#0.1
#使用softmax后，可以按照score得分高低来转换成概率大小，所有输出值相加为1:
#2.0     0.7
#1.0  -> 0.2
#0.1     0.1

#MSE均方差loss函数及其梯度计算
#参考资料：https://zhuanlan.zhihu.com/p/35707643
#下面例子中：x表示两个样本数据，每个数据是一个长度为4的tensor：[2,4]
x = tf.random.normal([2,4])
#输入数据的维度是4，输出节点我们定义为3维，表示3分类结果
w = tf.random.normal([4,3])
#bias初始化为0
b = tf.zeros([3])
#输出的label值,表示两个样本的真实label的class是2和0
y = tf.constant([2,0])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    #使用softmax计算概率
    prob = tf.nn.softmax(x@w +b, axis=1)
    #使用MSE计算loss
    loss = tf.reduce_mean(tf.losses.MSE(tf.one_hot(y, depth=3), prob))
#求解损失函数的梯度
grads = tape.gradient(loss, [w,b])
print("Gradients of w:\n", grads[0].numpy())
print("Gradients of b:\n", grads[1].numpy())

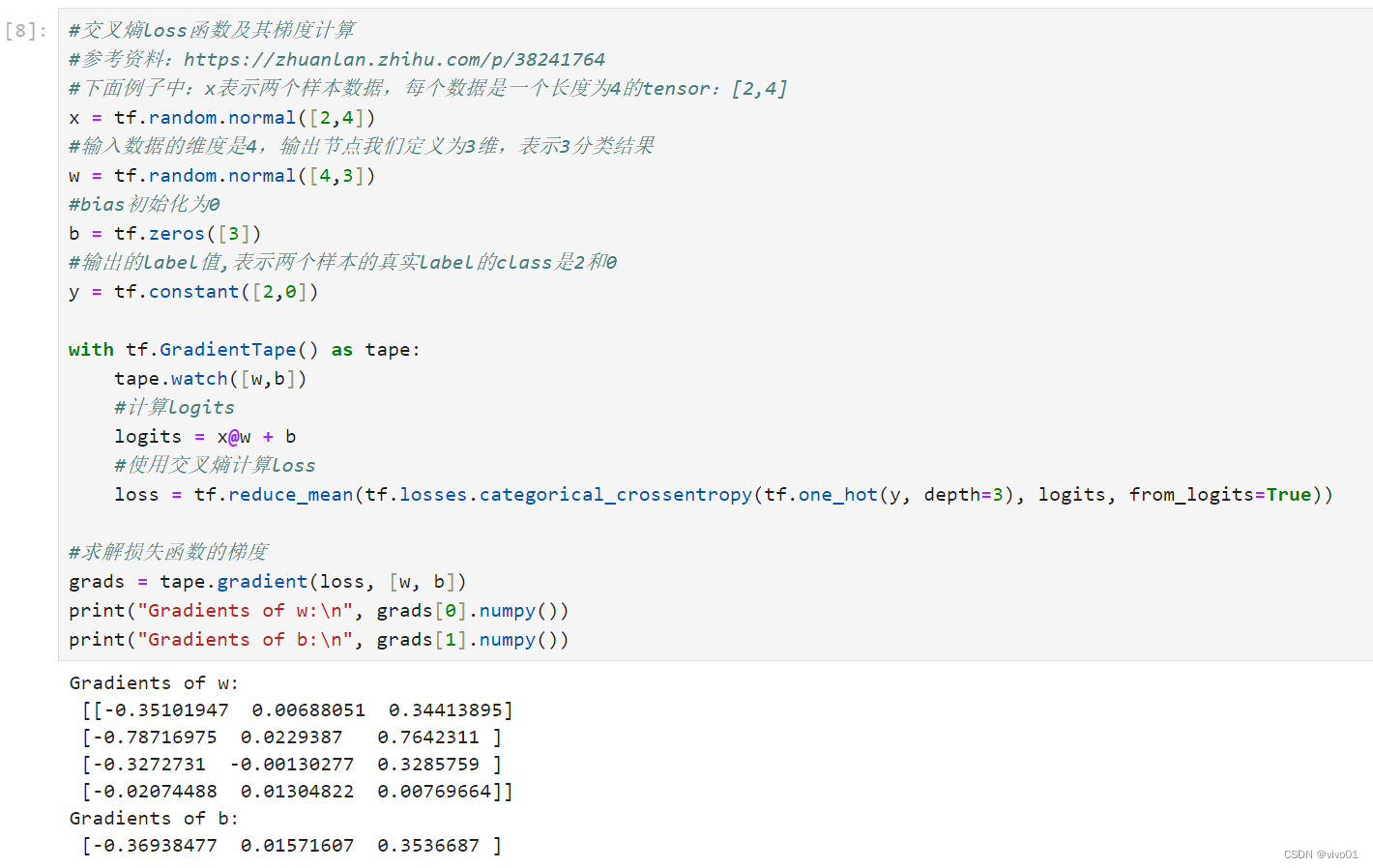
#交叉熵loss函数及其梯度计算
#参考资料：https://zhuanlan.zhihu.com/p/38241764
#下面例子中：x表示两个样本数据，每个数据是一个长度为4的tensor：[2,4]
x = tf.random.normal([2,4])
#输入数据的维度是4，输出节点我们定义为3维，表示3分类结果
w = tf.random.normal([4,3])
#bias初始化为0
b = tf.zeros([3])
#输出的label值,表示两个样本的真实label的class是2和0
y = tf.constant([2,0])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    #计算logits
    logits = x@w + b
    #使用交叉熵计算loss
    loss = tf.reduce_mean(tf.losses.categorical_crossentropy(tf.one_hot(y, depth=3), logits, from_logits=True))

#求解损失函数的梯度
grads = tape.gradient(loss, [w, b])
print("Gradients of w:\n", grads[0].numpy())
print("Gradients of b:\n", grads[1].numpy())

运行结果：