首页课程文章
无痕注入APC注入线程注入读写驱动注入技术句柄表进程线程系统调用保护模式内存管理远程CALL软件调试驱动封装云下发驱动开发FPS数据方框透视FPS方框FPS自瞄CED3DHOOKD3D绘制Imgui绘制DWM
内核课程驱动出租学习路线聊天室免责声明提问技巧

编程技术-使用神经网络拟合数学函数

推荐 原创

周杰伦

文章分类Android安全CTF对抗IOS安全阅读数 : 501阅读时长 : 9分钟

说明

这是一份练习代码，但感觉有点意思。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
import numpy as np
 
'''
使用神经网络拟合数学函数
能用数学函数，或者确定的算法解决的事情，自然是最精确的，往往也是最省力的，但是，对于复杂的函数、系统，很难找到一条漂亮的数学函数或者算法，这时候可以考虑数据拟合，而神经网络可以做这个事情。
'''
 
class Dot( object ):
     def forward( self , X, W):
         self .X = X
         self .W = W
         return np.dot(X, W)
 
     def backward( self , dout):
         return np.dot(dout, self .W.T), np.dot( self .X.T, dout)  # dX, dW
 
class Add( object ):
     def forward( self , D, B):
         return D + B
 
     def backward( self , dout):
         return np. sum (dout, axis = 0 )  #纵向求和
 
class Affine( object ):
     def __init__( self ):
         self .dot = Dot()
         self .add = Add()
 
     def forward( self , X, W, B):
         T = self .dot.forward(X, W)
         return self .add.forward(T, B)
 
     def backward( self , dout):
         dB = self .add.backward(dout)
         dX, dW = self .dot.backward(dout)
 
         return dX, dW, dB
 
class Sigmoid( object ):
     def forward( self , A):
         self .out = 1 / ( 1 + np.exp( - A))
         return self .out
 
     def backward( self , dout):
         return dout * ( 1.0 - self .out) * self .out
 
class Relu( object ):
     def forward( self , A):
         self .mask = (A< = 0 )
         A[ self .mask] = 0     #会破坏原参数，但是这次使用之后后面就没用了，所以破坏就破坏了，还能省点空间
         return A
 
     def backward( self , dout):
         dout[ self .mask] = 0
         return dout
 
class SoftmaxWithLoss( object ):
     def softmax( self , A):
         A = A - A. max (axis = 1 , keepdims = True )
         T = np.exp(A)
         return T / np. sum (T, axis = 1 , keepdims = True )
 
     def crossEntropyError( self , Z, Label):
         delta = 0.000000001
         return - np. sum (np.log(Z + delta) * Label) / Z.shape[ 0 ]
 
     def forward( self , A, Label):
         self .Z = self .softmax(A)
         self .Label = Label
         return self .Z, self .crossEntropyError( self .Z, Label)
 
     def backward( self , dout = 1 ):
         return ( self .Z - self .Label) * dout / self .Z.shape[ 0 ]
 
class MSELoss( object ):
     def forward( self , A, Label):
         self .A = A
         self .Label = Label
         # ∑( ∑(yi-xi)^2 )/batch_size
         return np. sum ((A - Label) * (A - Label)) / A.shape[ 0 ]    # A.shape[0] 为样本数，batch_size
 
     def backward( self , dout = 1 ):
         return 2 * ( self .A - self .Label) * dout / self .A.shape[ 0 ]
 
class MyNN( object ):
     def __init__( self ):
         self .lr = 0.01
         self .MAX_NUM = 1000000
 
     def buildThreeLayerNet( self , input_dim, output_dim):
         N0 = input_dim
         N1 = 10             #超参，为什么设置程这个数值，没啥理由，感觉
         N2 = 10
         N3 = output_dim
 
         self .W1 = np.random.randn(N0, N1)
         self .B1 = np.random.randn(N1)
 
         self .W2 = np.random.randn(N1, N2)
         self .B2 = np.random.randn(N2)
 
         self .W3 = np.random.randn(N2, N3)
         self .B3 = np.random.randn(N3)
 
         self .affine1 = Affine()
         self .activation1 = Sigmoid()  #对于浅层的简单网络，相对于 Relu ，激活函数使用 Sigmoid 似乎表达能力更强一些
         self .affine2 = Affine()
         self .activation2 = Sigmoid()
         self .affine3 = Affine()
         self .mseloss = MSELoss()
 
     def getMaxAbsValue( self , X):
         a = np. max (X)
         b = np. min (X)
         if b< 0 :
             b = - b
 
         ret = max (a,b)
         if ret = = 0 :
             ret = 0.0000001
         return ret
 
     def learn( self , X, Y):
         input_dim = len (X[ 0 ])
         output_dim = len (Y[ 0 ])
 
         self .MAX_X = self .getMaxAbsValue(X)
         self .MAX_Y = self .getMaxAbsValue(Y)
         X = np.array(X) / self .MAX_X
         Y = np.array(Y) / self .MAX_Y
 
         self .buildThreeLayerNet(input_dim, output_dim)
 
         for i in range ( 0 , self .MAX_NUM):
             A1 = self .affine1.forward(X, self .W1, self .B1)
             Z1 = self .activation1.forward(A1)
             A2 = self .affine2.forward(Z1, self .W2, self .B2)
             Z2 = self .activation2.forward(A2)
             A3 = self .affine3.forward(Z2, self .W3, self .B3)
             l = self .mseloss.forward(A3, Y)
 
             if i % 10000 = = 0 :
                 print (l)
 
                 if l< 0.0001 :
                     #print(Y)
                     #print(A3)
                     #print(self.predict(X))
                     break
 
             dA3 = self .mseloss.backward(dout = 1 )
             dZ2, dW3, dB3 = self .affine3.backward(dA3)
             dA2 = self .activation2.backward(dZ2)
             dZ1, dW2, dB2 = self .affine2.backward(dA2)
             dA1 = self .activation1.backward(dZ1)
             dX, dW1, dB1 = self .affine1.backward(dA1)
 
             #根据梯度调整权重与偏置
             self .W1 - = self .lr * dW1
             self .B1 - = self .lr * dB1
             self .W2 - = self .lr * dW2
             self .B2 - = self .lr * dB2
             self .W3 - = self .lr * dW3
             self .B3 - = self .lr * dB3
 
     def predict( self , X):
         X = np.array(X) / self .MAX_X
 
         A1 = self .affine1.forward(X, self .W1, self .B1)
         Z1 = self .activation1.forward(A1)
         A2 = self .affine2.forward(Z1, self .W2, self .B2)
         Z2 = self .activation2.forward(A2)
         A3 = self .affine3.forward(Z2, self .W3, self .B3)
         return A3 * self .MAX_Y
 
class FitFx( object ):
     def fx1( self , x):
         # f(x)=x-5
         return x - 5
 
     def fx2( self , x):
         # f(x)=(x-5)^2
         return (x - 5 ) * * 2
 
     def fx3( self , x):
         # f(x)=(x-5)^3+1
         return (x - 5 ) * * 3
 
     def fx4( self , x):
         # f(x)=(x-5)^3+1
         return (x - 5 ) * * 4
 
     def fx_xor( self , x1, x2):
         return x1^x2    # 异或
 
     def fit11( self , fx):
         print (fx)
         X = [[i] for i in range ( 0 , 11 )]
         print (X)
         Y = [[fx(a[ 0 ])] for a in X]
         print (Y)
 
         nn = MyNN()
         nn.learn(X,Y)
         print (nn.predict(X))
         #print(nn.predict([[1.2],[8.5]]))
 
     def fit21( self , fx):
         print (fx)
         X = [[d1,d2] for d1,d2 in [( 0 , 0 ), ( 0 , 1 ), ( 1 , 0 ), ( 1 , 1 )]]
         print (X)
         Y = [[fx( * a)] for a in X]
         print (Y)
 
         nn = MyNN()
         nn.learn(X,Y)
         print (nn.predict(X))
 
 
def main():
     m = FitFx()
     #m.fit11(m.fx1)
     m.fit11(m.fx2)
     #m.fit11(m.fx3)
     #m.fit11(m.fx4)
 
     #m.fit21(m.fx_xor)
 
if "__main__" = = __name__:
     main()

效果
图片描述
图片描述



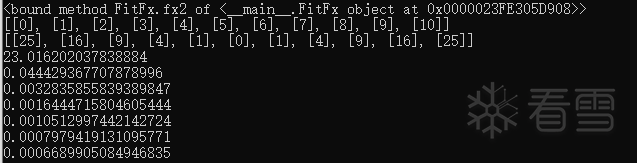
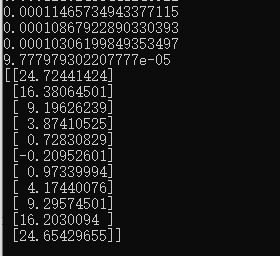
更多【使用神经网络拟合数学函数】相关视频教程：www.yxfzedu.com




相关文章推荐

记录自己的技术轨迹
文章规则：
1)：文章标题请尽量与文章内容相符
2)：严禁色情、血腥、暴力
3)：严禁发布任何形式的广告贴
4)：严禁发表关于中国的政治类话题
5)：严格遵守中国互联网法律法规
6)：有侵权,疑问可发邮件至service@yxfzedu.com
近期原创 更多

Markdown Editor

友情链接
内核结构FAQ
免责声明
课程目录
Windows内核
游戏逆向(FPS)
技术交流QQ群
342478842215039827137189196
314055665159620936
www.yxfzedu.com是一个分享游戏安全,游戏外挂与反外挂,游戏驱动保护的视频网站！
接各种驱动定制如：游戏读写驱动，软件内存保护，防止调试等功能定制。
出租读写驱动，调试驱动，无痕注入支持各种游戏。
邮箱：service@yxfzedu.com
QQ：851920120
特别说明：不接游戏数据分析，外挂编写，登陆协议等类似业务。