算法-数据结构·排序
推荐 原创1. 排序的概念及运用
1.1 排序的概念
排序:排序是将一组“无序”的记录序列,按照某个或某些关键字的大小,递增或递减归零调整为“有序”的记录序列的操作
稳定性:假定在待排序的记录序列中,存在多个具有相同关键字的记录,若经过排序,这些记录的相对次序保持不变。及在原序列中, r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的
内部排序:数据元素全部放在内存中的排序
外部排序:数据元素太多,不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
1.2 常见的排序算法
插入排序:直接插入排序,希尔排序
选择排序:选择排序,堆排序
交换排序:冒泡排序,快速排序
归并排序:归并排序
2. 常见排序算法的实现
2.1 插入排序
基本思想:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列,这个过程就像我们在整理扑克牌一样
2.1.1 直接插入排序 O(N^2)
当插入第 i (i >= 1) 个元素时,前面的 array[0],array[1] …… array[i-1] 已经排好序,此时用 array[i] 的排序码与 array[i-1],array[i-2],…… 的排序码顺序进行比较,找到插入为止及将 array[i-1] 插入,原来位置上的元素顺序后移
实现:

直接插入排序的特性总结
1. 元素集合越接近有序,直接插入算法的时间效率越高
2. 时间复杂度 0(N^2)
3. 空间复杂度 O(1)
4. 稳定的排序算法
2.1.2 希尔排序 O(N^1.3)
在学希尔排序之前,我们先对比一下同为 O(N^2) 量级的两个排序,插入和冒泡。
他俩的结构很像,都是将数据们分成:已经排好的区域,和还没排好的区域。但是在每轮排序过程的处理方案时出现了分歧,冒泡排序是一定会再次遍历一遍那块没排好的区域,然后将一个数据落入已经排好的区域,但是插入排序有可能不用完全遍历那块已经排好的区域,甚至只用访问一次那块区域 (tmp >= a[end]),就可以从没排好的区域中落一个数据进入已经排好的区域。换句话说插入排序有很强的适应性,它几乎每轮排序都不是最坏的情况,甚至都还不错,这是冒泡排序达不到的,冒泡排序只会把每轮排序都当作最坏的情况处理。
正是因为这个原因,在处理大量数据的绝大多数情况下,插入排序的速度要比冒泡排序块很多。或者说得益于插入排序的第一个特性,元素集合越接近有序,直接插入算法的时间效率越高,在绝大多数任务中插入排序的效果明显好于冒泡排序。
那么我们该如何放大这个优势,优化插入排序,让其排序速度更快。这时聪明的希尔就有了这样一个思路,将排序过程分成两步。第一步是预排序:将数据们都整理的越来越有序,第二步是执行一次插入排序,经过这两步操作数据集合就有序了。
那么有的同学这时候就开始怀疑了,这也没看出来什么神奇的思路,这个希尔排序怎么就好了,那么我展示一下用我们学过的四种排序处理 100,000 个随机数据的用时(ms),1,000,000个数据冒泡实在是跑不出来我们就看前3个,10,000,000个数据插入也跑不动了我们看剩下两个
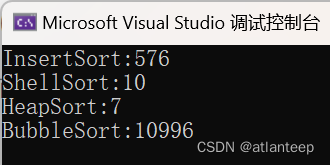

100,000个随机数据 1,000,000个随机数据
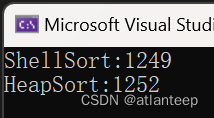
10,000,000个随机数据
看到了吗,希尔排序对于插入排序产生了巨大的优化,甚至在数据量巨大的情况下,其速度竟然超过了堆排序。
这个测试就是开了几块空间往里头填相同的随机值,让这几种排序方法分别给这几块空间进行排序,记录了各自排序的时长,这个测试时长的代码挺简单的,这里我就不写了,如果想要可以评论区说一下
2.1.2.1 预排序
预排序的思路就是选定一个整数n,把待排序集合中的所有数据分成n组,所有距离为n的数据分在同一组内,并对每一组内的数据进行排序。这样做的好处就是让大的数尽快到后面,小的数尽快到前面,选定的整数n越大,数字移动的越快,但是数据集合越不接近有序
这里我们选定整数为3,因此所有数据被分成了3组 (黑、红、蓝)

接下来就是给这三组数据分别排序,我们一步一步的展示如何写出一个排序
第一步,是写出一次排序的代码

这里我们就能发现其实这跟插入排序的一轮排序是一样的,只是将自增自减的地方改成了加gap减gap
第二步,将一组排序

到这里我们将黑色组完成了排序,其实就是加了一层循环让每次排序跑起来
第三步,将每组都排序
首先我们能想到的就是再套一层循环控制排完一组再去排下一组

但是我们还可以这样操作:控制完这组的第一个再控制下一组的第一个,每组第一个控制完之后,控制每组的第二个,这样并不会有负面影响,就相当于将每组的排序拆开来进行,大家可以体会一下这个过程,这样就只用一层循环就能解决问题

但是他俩的效率是一样的,只是这种方法代码量小了一点,还有就是这种方法看起来相当的天才
到这里预排序就完成了,现在的数据集合已经变成了一个比较有顺序的集合了
2.1.2.2 控制gap完成排序
我们前面提到过gap越大,数据跳的越快,大的数据更快到后面,小的数据更快到前面,但是越不接近有序。gap越小数据跳的越慢,但是越接近有序,gup == 1时就是插入排序,数据集合直接就有序了。
所以说我们要靠控制合适的gap值来达到时间效率的提升,这时有人想到了用这样的方法
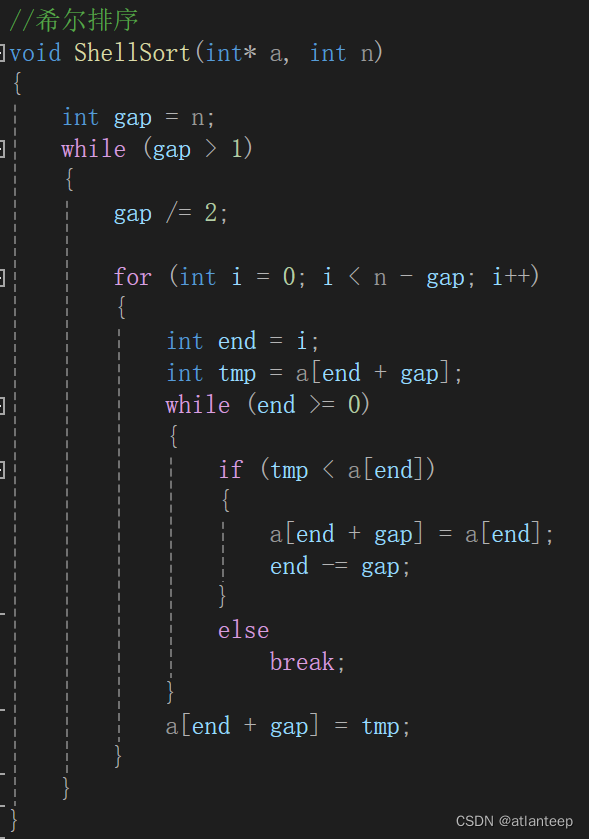
让gap每次除2,让数据元素处理的很有调理,还保证了最后一个值一定是1 ,因为一个大于1的数除2商一定为1。
后来还有人提 gap = gap / 3 + 1 的方案,总之到现在为止还没有哪一种主张得到了充分的证明。
对于希尔排序的时间复杂度计算到现在也还没有定论,有人利用大量的实验统计出当数据集合容量n很大时,时间复杂度大概在 O(N^1.25) 到 O(1.6*N^1.25) 之间,为了好记我就认为是 O(N^1.3)
最后,希尔排序是不稳定的排序算法
2.2 选择排序
基本思想:
每一次从待排序的元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到所有待排序的元素都处理完
2.2.1 直接选择排序 O(N^2)
这里我们每次找出最大和最小两个数据分别弄到数组尾部和头部,这样能节省一半的循环操作。因为我们每次排序都是交换两次数据,那就有可能刚交换完一次数据之后第二次又交换回去了,这样排序就出错了,这点要特别注意一下
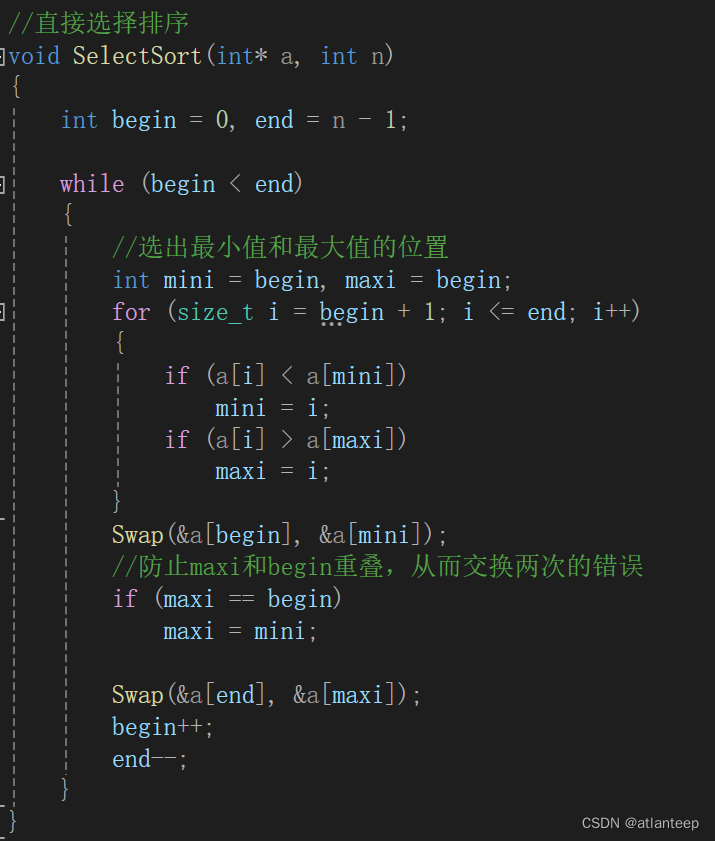
直接选择排序是不稳定排序算法,因为可能把很前面的一个大数据换到很后面,打乱了原本的顺序
2.2.2 堆排序 O(N*logN)
堆排序我们刚讲完,这里就展示一下代码

堆排序是不稳定排序算法
2.3 交换排序
基本思想:
根据元素集合中两个元素的大小比较结果来对换两个元素的位置,交换排序的特点是将较大的值向集合尾部移动,较小的值向集合首部移动
2.3.1 冒泡排序 O(N^2)
这个太简单了,直接上代码

冒泡排序是稳定的排序算法
2.3.2 快速排序 O(N*logN)
快速排序是霍尔于1962年提出的一中二叉树结构的交换排序方式,其基本思想为:任取待排序元素序列中的某元素值作为基准值,利用基准值将元素集合分割成左子集合、基准值、右子集合。小于基准值的元素都放到左子集合,大于基准值的元素都放到右子集合。然后左右子集合重复该过程,直到所有元素都到达自己相应的位置上。
下面我们解释一下,当元素右边都是小于它的值,左边都是大于它的值,那么我们是不是就可以认为这个元素已经到达了它相应的位置上。之后我们再将基准值的左右子集合中找到一个数放到它相应的位置上,不停的递归这一过程,最后元素集合不就有序了吗,这是快速排序的核心思想,大家可以理解一下。
这里我直接展示一次排序的代码,然后咱们根据这个代码讲解一下
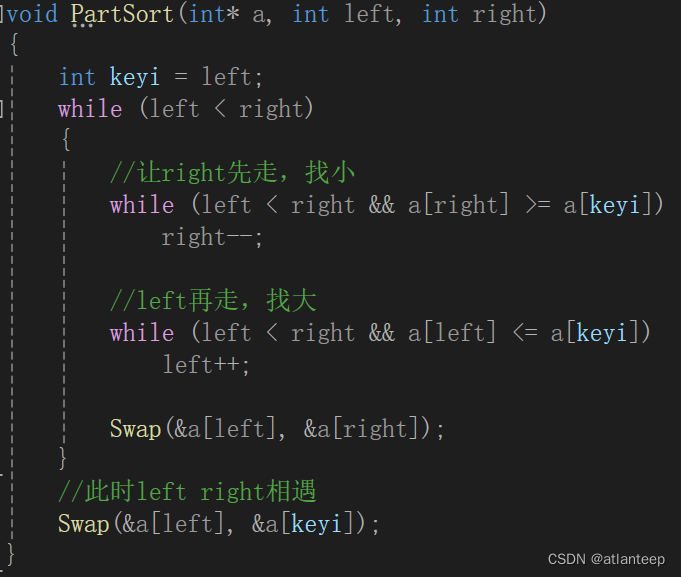
这里我们搞一组数据,一般都是将第一个数据设成基准值,或者说关键值

然后我们让right指针先走,当找到小于基准值的数据时就停下来,然后再让left指针走,找到大于基准值的数据停下来,然后交换left指针和right指针指向的两个元素

就这样一直让左右指针找下去,直到他俩相遇,此时把它们同时指向的元素和基准值交换,因为要交换基准值,所以我们记录基准值时并不是记录它的值,而是记录它所在的下标keyi,否则就根形参一样不会正确的交换。
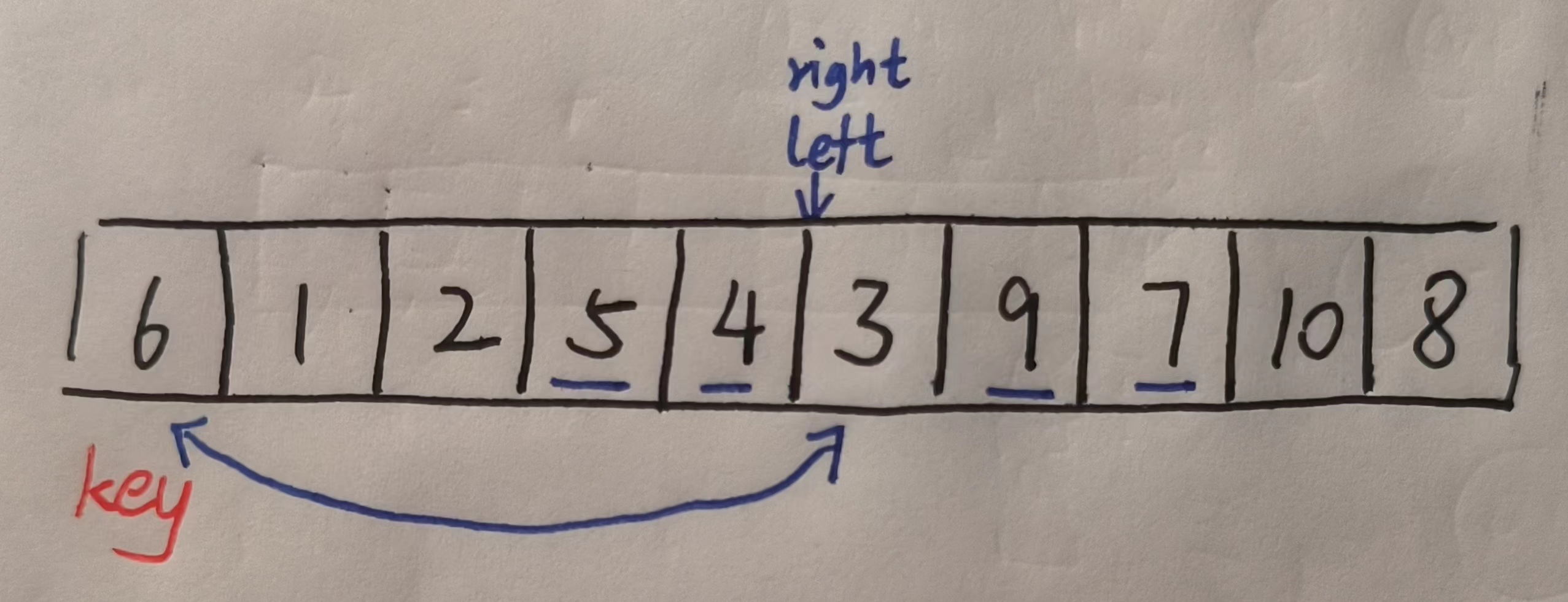
我知道,此时一定有同学会怀疑,为啥最后一步可以就这么直接交换呢,万一俩指针同时指向的值比key大怎么办。
其实,结论是俩指针同时指向的值是一定比key小,大家可以思考一下。
只要left和right之间有比key小的值,那么经过交换后,这个比key小的值一定会到left指针底下,此时如果left和right之间没有比key小的值了,那么下一次移动right就会停到left指针上面,此时他俩同时指向的值因为上一步的筛选一定比key小,这就是让right指针先走的特性。
那如果从一开始left和right之间就没有比key小的值,那么right指针就会直接走到left指针上,也就是key上,此时交换一俩指针同时指向的值和key就相当于没交换,还是正确的。
所以说经过这一次排序之后数组就变成了这样。
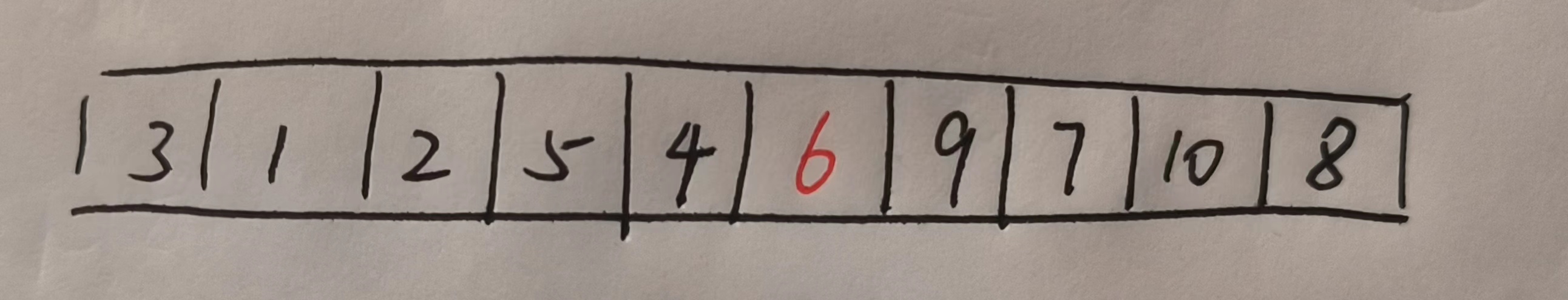
此时6到达了它相应的位置,之后的排序就是去递归处理6左边的区域和右边区域即可,注意左右区域是不包括key的
那么递归的最小子问题就是没有区域或者区域里只有一个值。

快排是不稳定的排序算法
2.3.2.1 快速排序优化
我们先跑一下快排,看看排1,000,000个数据和10,000,000个数据的用时
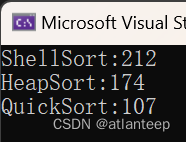

1,000,000个数据 10,000,000个数据
我们发现在数据完全随机的情况下,快排的效率还是很不错的,同样是二叉结构它比堆排块的原因是堆排的建堆是有些消耗的。
我们思考一下快速排序的时间复杂度到底是多少,因为它的思路于二叉树相同,所以说如果每次选出的key值都可以到区域最中间的情况是最好的,因为这种情况完全符合二叉结构,那么此时的时间复杂度就是 O(N*logN)。但是如果情况较坏,就是说数据集合是有序或者接近有序的情况下,时间复杂度就会来到 O(N^2)。
那么我们该如何优化这一缺陷,事实上我们可以在left和right控制的区间中随机选一个数,与left指向的数据交换位置,就像这样,我们成这种方案叫随机选key
那么此时可能有人就认为这种随机的方法还是不靠谱,还是有几率出现最坏的情况,所以就又有人提出另一种解决方案叫三数取中
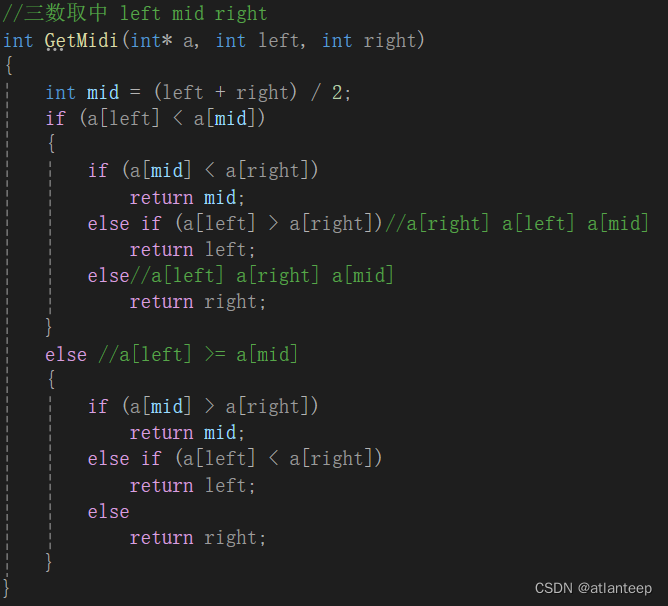
这段函数让我们从left到right区间取出了一个既不可能是这段区域中的最大值也不可能是最小值的数据的下标,下一步到了快排函数中让这个下标指向的数据与a[left]交换就行了,后面的代码的处理方案与随机选key是一样的
这个子函数的作用就是保证了取出来的值一定不是最大值也不是最小值,也就是说这样一来就一定不会出现最坏情况了,同时如果给出的任务集合是有序或接近有序的情况下,一下子就遍成了三数取中方案的最好情况
其实随机选key和三数取中两个方案,还是三数取中效率上好一点,但是随机选key的代码较短,最后还是根据实际情况自行取舍吧
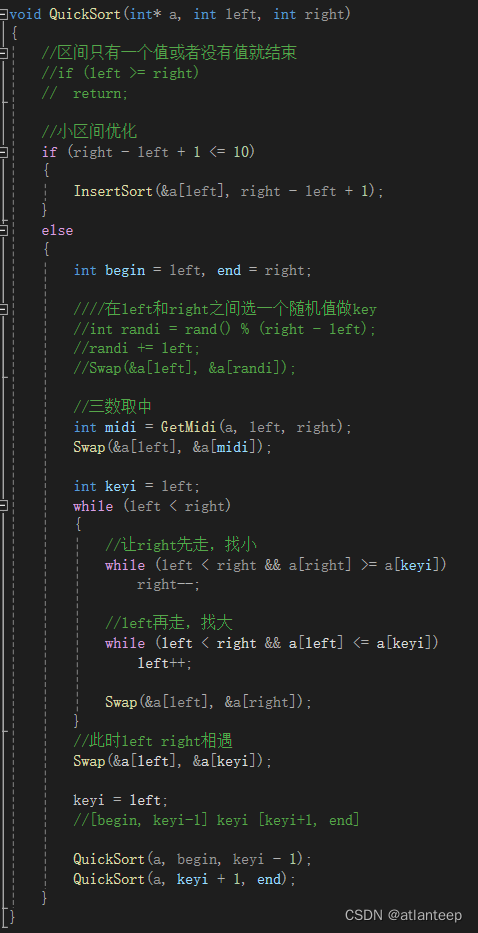
最后还有一种叫小区间优化的方案,这个优化方案与随机选key和三数取中优化的地方是不一样的,并且这个方案的优化效果不明显。
我们知道二叉递归,如果是一个满二叉树的话,最后一层的递归次数占总次数的50%,倒数第二层的递归次数占总次数的25%,也就是说后三层递归节点占了整颗树的87.5%。因此有人提出也许我们不需要递归的那么深,就是说不用非得让区间中的数据只剩一个或者没有再返回,可以让区间中还剩10个值的时候,我们给这10个值插入排序就行了。为什么选择插入排序,因为数据量不大,不用使用堆排序或希尔排序,抛去他俩肯定就插入最好了。
2.3.2.2 双指针快排法
这种双指针的方法是后人在希尔大佬的思想下延伸出来的另一种快排写法,这种写法的代码量被大大缩减了,同时时间效率相同
一样的,还是先选好一个关键值key,然后创建prev指针和cur指针

当cur指向的值大于等于key cur指针向后移动一位
当cur指向的值小于key prev指针向后移动一位,同时交换 prev 和 cur 指向的两个值,然后再将cur指针向后移动一位
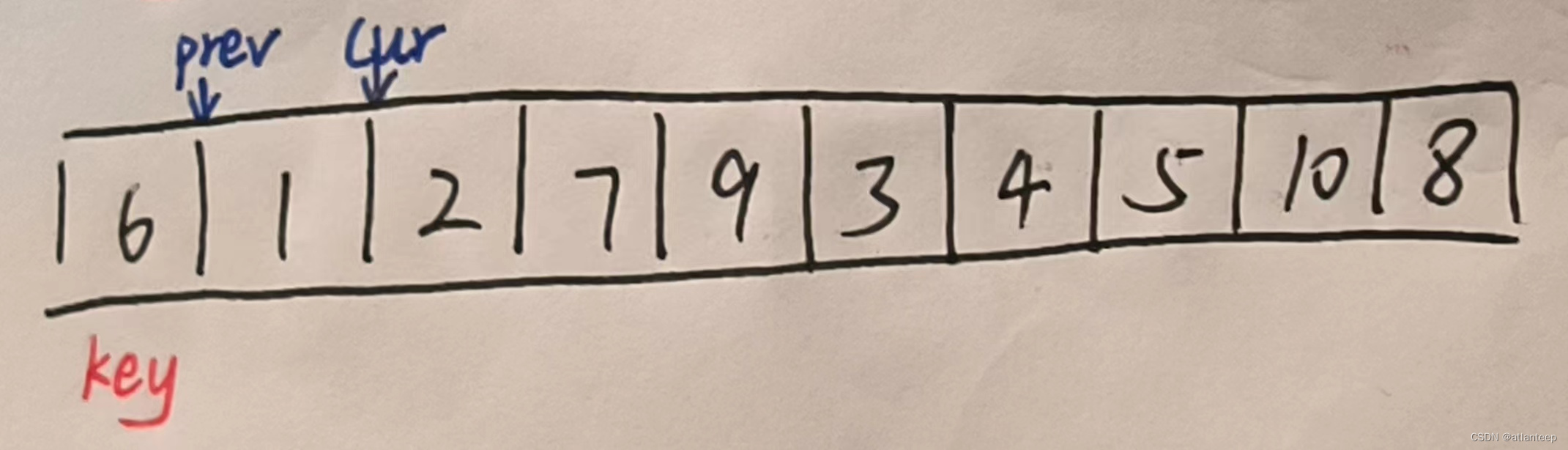
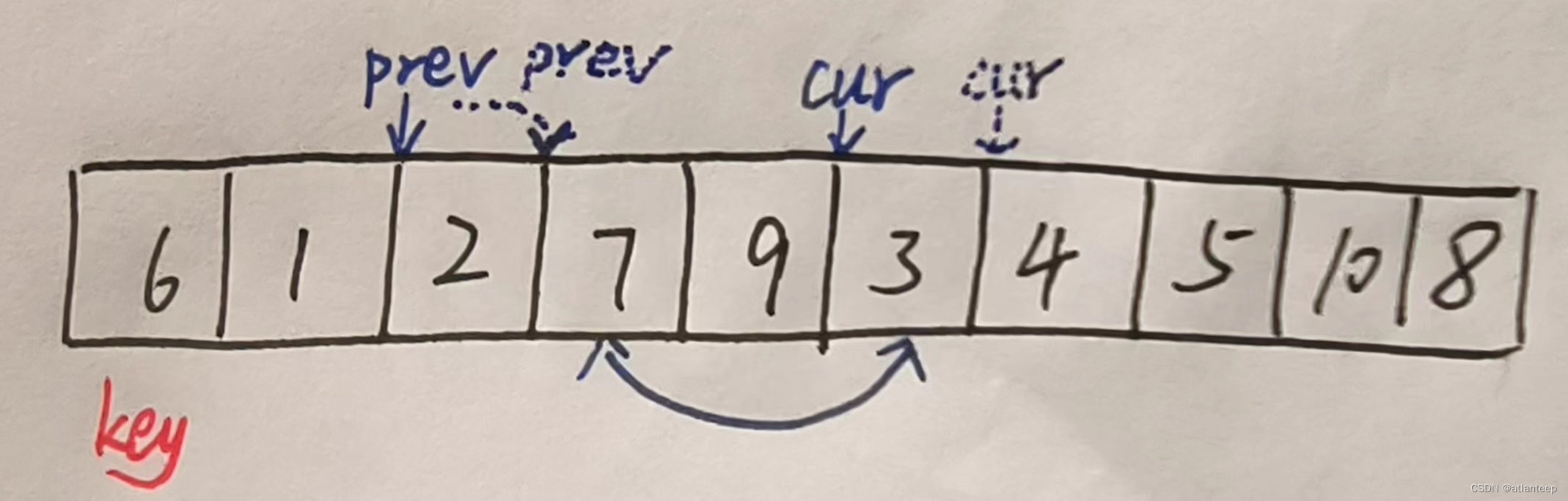
最后当cur遍历完整个数组之后就变成了这样,然后我们将key与prev指向的数据交换

此时的效果就是key到达了它对应的位置了。
这个放方法的关键就是保证了prev指针前面的元素都小于key(key除外),最后当cur指针遍历完数组的时候数组中所有小于key的数据都会出现在prev指针之前(key除外),并且prev指向的元素一定小于key,或者压根就是key。大家可以多走读几遍,理解一下这里面的逻辑 。
我们直接上代码

2.3.2.3 非递归快排法
如何绕开递归来实现快排呢,我们需要借助到栈。首先将需要排序的左右区间压入栈中,处理完后将这对控制区间的数字出栈,此时又出现了两个区间,我们先将右区间压栈,再将左区间压栈。然后取栈顶元素,取到了左区间进行处理并出栈,此时又出现两个区间······如此操作下去,如果区间中只有一个或没有值就不入栈,最后栈为空就说明都处理完了,记得销毁栈。
这里我们用双指针的方式处理一次排序
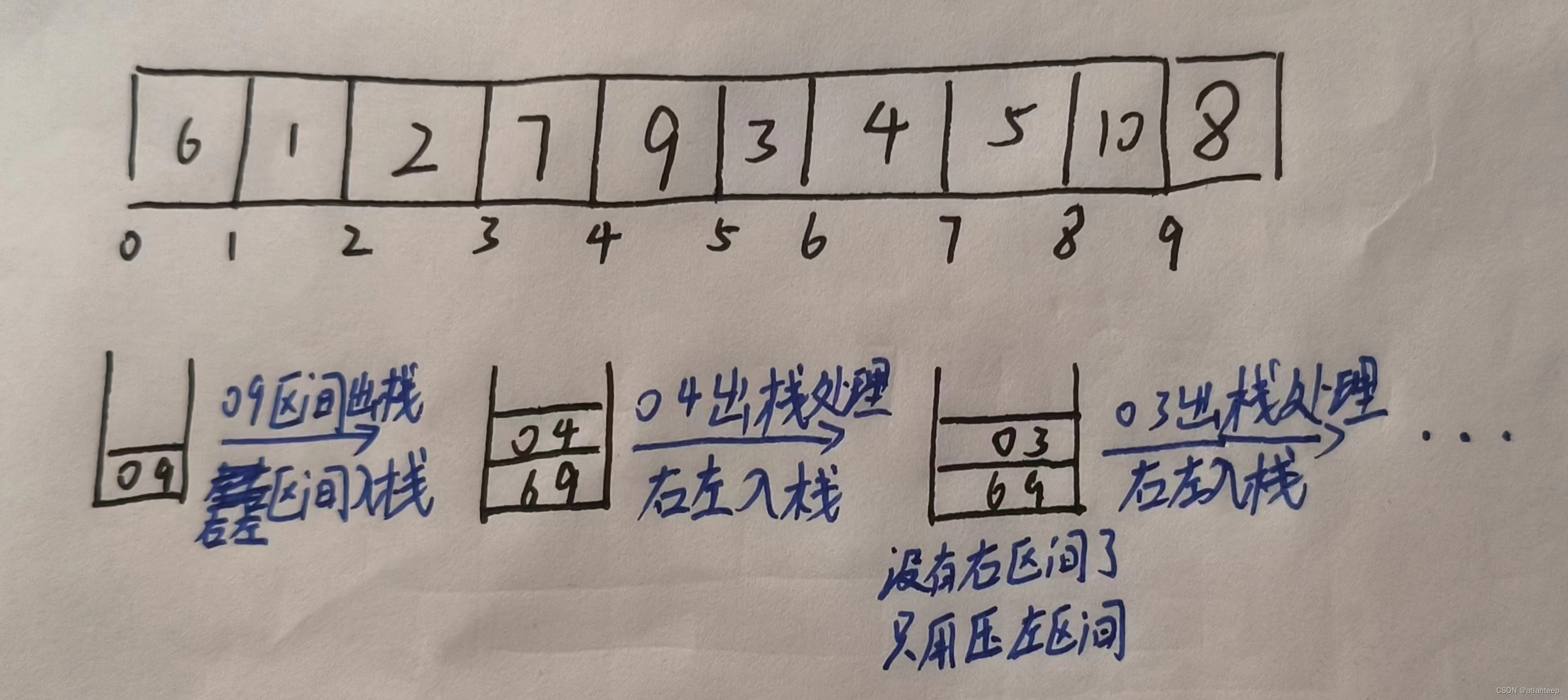
这里我给出的数据集合案例不太好,大家能明白是什么意思就行,其实这就是用栈后进先出的特点实现了类似递归的功能。
再实际敲代码的时候我们要不要把栈中元素的类型改成一个二元数组来表示区域呢?其实不必,我们只要保证:先压右边界再压左边界对应先取左边界再取右边界的顺序就好。进两个区域的时候也同理,一直保证先压右区域再压左区域,相当于后处理右区域,先处理左区域。
处理就是单趟排序,将key放到它对应的位置
这个用栈模拟递归的思路还是很巧妙的,那我们为什么要有这种非递归的需求呢?是因为函数栈帧(函数调用所需空间)是建立在操作系统的栈(这个栈与我们自己写的栈是完全两回事)上的,这个操作系统的栈比较小,如果我们的递归深度太深就会导致栈溢出,从而崩掉。而我们自己写的栈是建立在堆区上的,这块区域相对来说就比较大了,不会出现类似栈溢出的问题。
事实上非递归还可以用队列实现,队列拥有先进先出的特点,那么在实现的时候我们就能看到队列是以层序遍历的结构在进行处理的,先处理左区域,然后把左区域中的左右区域入队列,pop掉左区域,然后取队头就是右区域,处理完之后同样把右区域中的左右队列入进来,pop掉右区域。此时一层就处理完了,然后接下来去处理下一层。只是这种处理结构与递归时的结构思路不同,我就不重点讲解了。
2.4 归并排序 O(N*logN)
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已经有序的子序列合并,得到完全有序的数列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
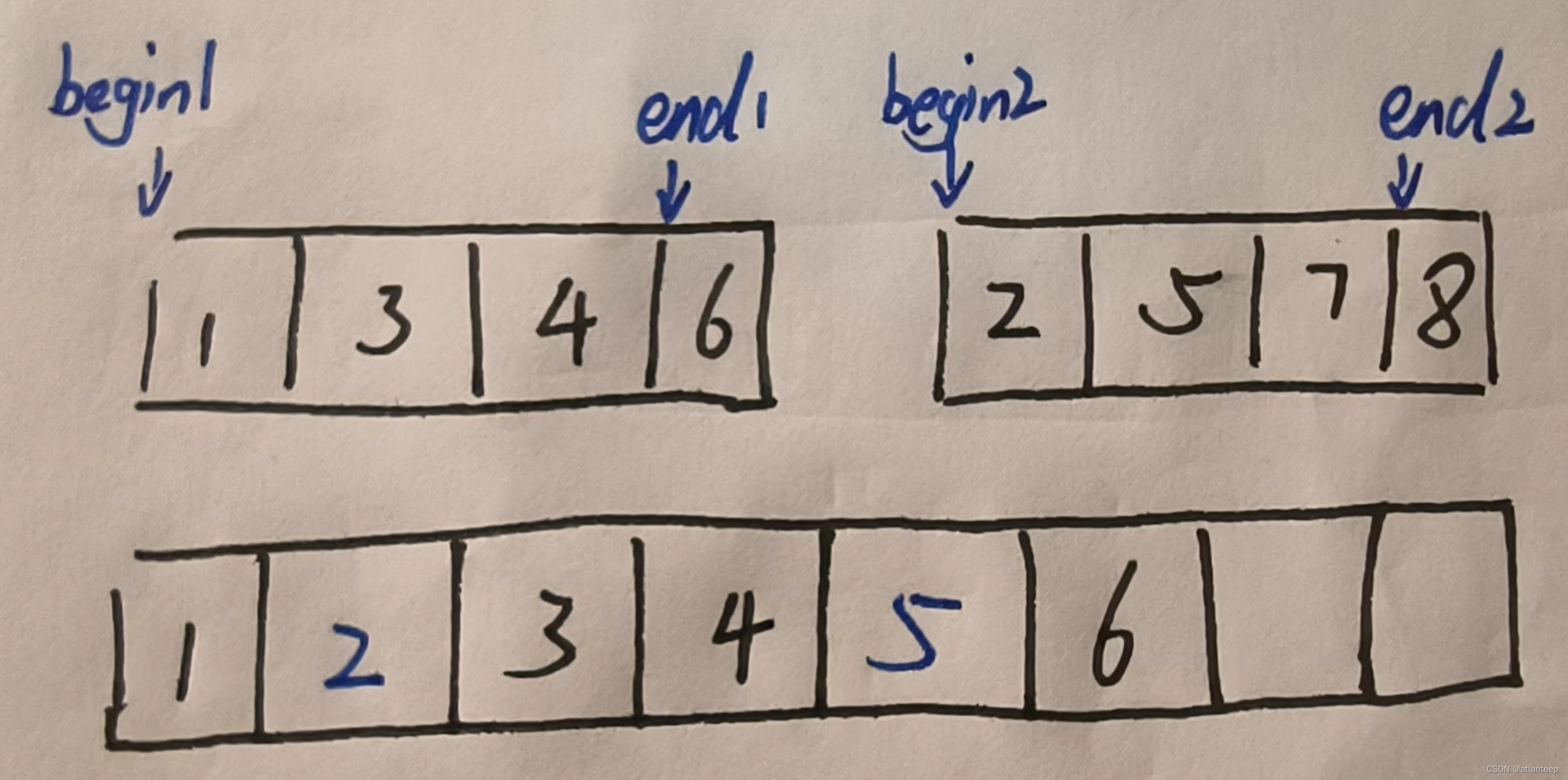
单趟归并中,我们拿到两个有序的数组之后,用4个指针控制着向后走,哪个begin指针指示的数据小就入到新开辟的空间tmp中,直到有一个数组遍历完,再把另一个数组剩下的数据粘到新开辟的空间tmp中
归并排序我们还是要用分治的思想借助递归完成,当分开的区域中就剩一个数据的时候就可以开始返回了
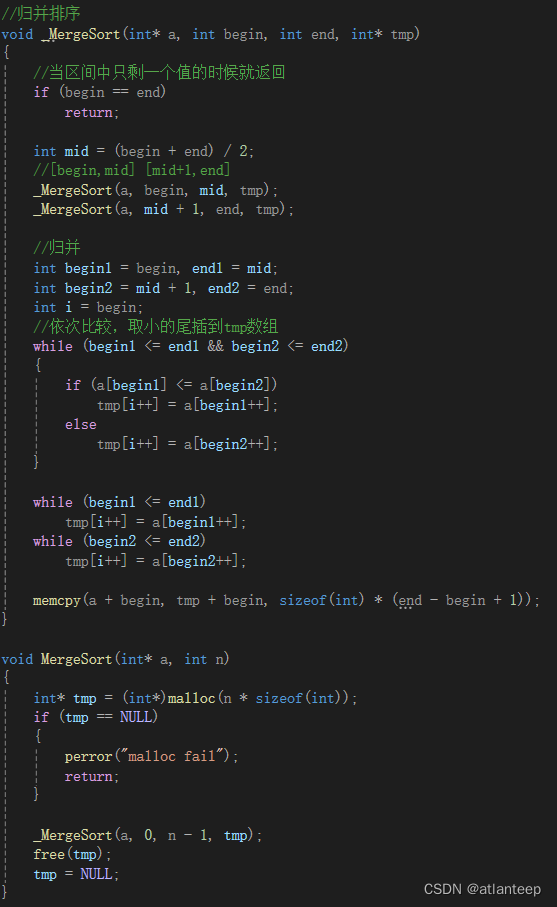
归并排序的思路很简单,但是其中的一些控制细节需要用点心
归并排序是稳定的排序算法
2.4.1 非递归归并
如果像快排那样用栈实现的话,我们想一下就会发现不现实,因为快排单趟排完之后就不用那块区间了,或者说快排的排序发生在逻辑树展开的过程中,等逻辑树到达了所有叶节点(区间大小<=1)之后排序就结束了。但是归并的排序是发生在逻辑树回归的过程当中,将区域从1开始慢慢扩大,每扩大一次就实现一次单趟归并,我们都将上一块区域的界限pop掉了,找不到上一级的区域界限那就归不动了。
所以我们要换一种思路,将相邻数据区间进行归并,这样做的时间复杂度不变,但是思考方案确实与递归不同了

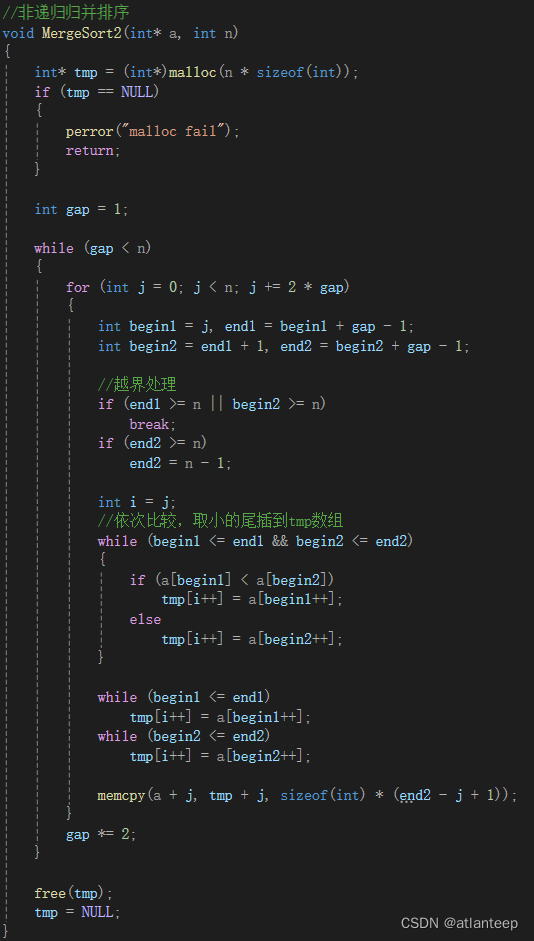
非递归的主要难点不是思路,而是越界处理的细节控制
2.5 非比较排序
前面我们讲到的排序都是比较排序,核心都是通过比较大小进行排序的。而非比较排序的核心不在比较,常见的非比较排序有:计数排序、基数排序、桶排序,非比较排序都是小众且局限的排序方案,这里我们仅讲解计数排序
2.5.1 计数排序 O(N)
计数排序的思路很简单,就是再弄一个计数数组,下标对应任务数组的值,然后扫描任务数组,比如任务数组出现了一个6,那就在计数数组下标为6的位置加1。如此做的意义就是任务数组中一个值出现了几次,都会被计数数组在相应的映射位置上统计下来。
这种方案听起来是不是特别简单,而且时间复杂度就是O(N),空间复杂度是O(N)。但是这个方案有两个局限性:第一是只适合排整形,而实际应用中很少有这种需求;第二是只适合任务数组的值较为集中的情况,否则计数数组要开很大。
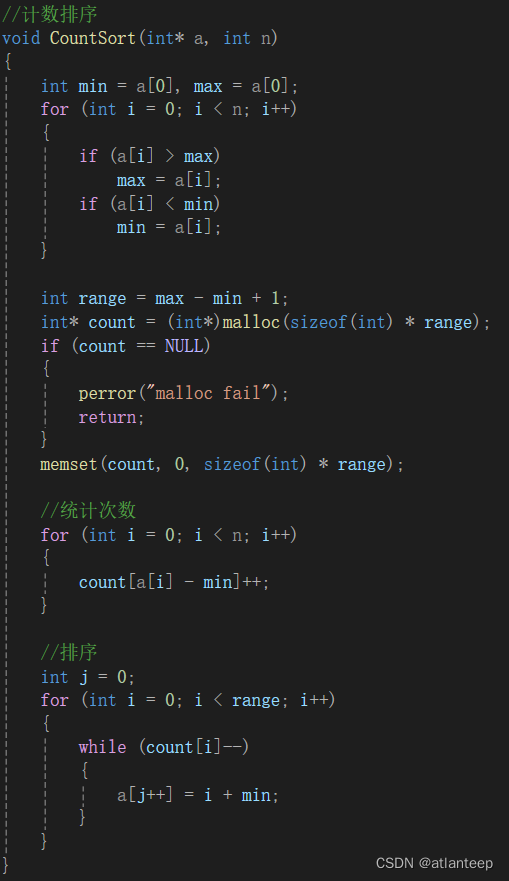
这里我还是简单说一下基数排序和桶排序吧,它们的原理是一样的,都是先排个位,再排十位,再排百位,这样往上排。区别就是基数排序直接用变量存储每次排序的结果,而桶排序是用链表存储的,比如个位是0的用链表串成一串挂起来,个位是1的用链表串成一串挂起来这样。这两种排序方案效率既低,消耗又大,同时还没有像冒泡排序那样的教学意义,总之就是很鸡肋。
3. 本节完整代码
Sort.h
#pragma once
#include"Stack.h"
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
//时间计算
void TestOp();
//打印数组
void PrintArry(int* a, int n);
//交换
void Swap(int* p1, int* p2);
//插入排序
void InsertSort(int* a, int n);
//希尔排序
void ShellSort(int* a, int n);
//直接选择排序
void SelectSort(int* a, int n);
//堆排序
void HeapSort(int* a, int n);
//快排
void QuickSort(int* a, int left, int right);
//双指针快排
void QuickSort2(int* a, int left, int right);
//快排非递归
void QuickSort3(int* a, int left, int right);
//归并排序
void MergeSort(int* a, int n);
//非递归归并排序
void MergeSort2(int* a, int n);
//计数排序
void CountSort(int* a, int n);
//冒泡
void BubbleSort(int* a, int n);
Sort.c
#include"sort.h"
//打印数组
void PrintArry(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//插入排序 O(N^2)
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
//变量end指示有序数列的最后一个位置
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
break;
}
a[end + 1] = tmp;
}
}
//希尔排序 O(N^1.3)
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap /= 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
}
//直接选择排序
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
//选出最小值和最大值的位置
int mini = begin, maxi = begin;
for (size_t i = begin + 1; i <= end; i++)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
Swap(&a[begin], &a[mini]);
//防止maxi和begin重叠,从而交换两次的错误
if (maxi == begin)
maxi = mini;
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
//堆排序 O(N^logN)
void AdjustDown(int* a, int n, int parent)
{
//假设法,选出大的孩子
int child = parent * 2 + 1;//假设左孩子大
while (child < n)//当child>=size时出数组了说明是叶子
{
if (child + 1 < n && a[child + 1] > a[child])
{
//找到小的那个孩子
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
//数组直接建大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
AdjustDown(a, n, i);
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
//快速排序
//三数取中 left mid right
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])//a[right] a[left] a[mid]
return left;
else//a[left] a[right] a[mid]
return right;
}
else //a[left] >= a[mid]
{
if (a[mid] > a[right])
return mid;
else if (a[left] < a[right])
return left;
else
return right;
}
}
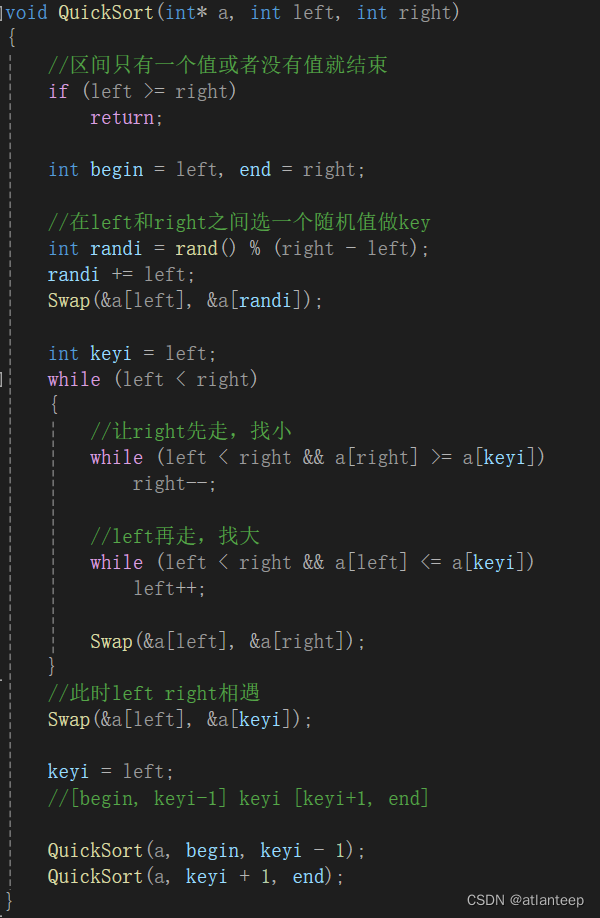
void QuickSort(int* a, int left, int right)
{
//区间只有一个值或者没有值就结束
if (left >= right)
return;
//小区间优化
//if (right - left + 1 <= 10)
//{
// InsertSort(&a[left], right - left + 1);
//}
else
{
int begin = left, end = right;
在left和right之间选一个随机值做key
//int randi = rand() % (right - left);
//randi += left;
//Swap(&a[left], &a[randi]);
//三数取中
int midi = GetMidi(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
//让right先走,找小
while (left < right && a[right] >= a[keyi])
right--;
//left再走,找大
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
}
//此时left right相遇
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}
//双指针快排
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
//[left, keyi-1] keyi [keyi+1, right]
QuickSort2(a, left, keyi - 1);
QuickSort2(a, keyi + 1, right);
}
//快排非递归
void QuickSort3(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
//栈不为空就说明还没处理完
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
//走单趟排序
int keyi = begin;
int prev = begin;
int cur = begin + 1;
while (cur <= end)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
//[begin, keyi-1] keyi [keyi+1, end]
//先进右再进左
if (keyi + 1 < end)
{
//进右
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi - 1)
{
//进左
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
STDestory(&st);
}
//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//当区间中只剩一个值的时候就返回
if (begin == end)
return;
int mid = (begin + end) / 2;
//[begin,mid] [mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
//依次比较,取小的尾插到tmp数组
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
tmp[i++] = a[begin1++];
else
tmp[i++] = a[begin2++];
}
while (begin1 <= end1)
tmp[i++] = a[begin1++];
while (begin2 <= end2)
tmp[i++] = a[begin2++];
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
//非递归归并排序
void MergeSort2(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int j = 0; j < n; j += 2 * gap)
{
int begin1 = j, end1 = begin1 + gap - 1;
int begin2 = end1 + 1, end2 = begin2 + gap - 1;
//越界处理
if (end1 >= n || begin2 >= n)
break;
if (end2 >= n)
end2 = n - 1;
int i = j;
//依次比较,取小的尾插到tmp数组
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[i++] = a[begin1++];
else
tmp[i++] = a[begin2++];
}
while (begin1 <= end1)
tmp[i++] = a[begin1++];
while (begin2 <= end2)
tmp[i++] = a[begin2++];
memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
//计数排序
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
perror("malloc fail");
return;
}
memset(count, 0, sizeof(int) * range);
//统计次数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}
//冒泡 O(N^2)
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n - 1; j++)
{
int flag = 0;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
flag = 1;
}
}
//当一趟冒泡结束后发现没有进行数据交换
//说明已经有序了
if (flag == 0)
break;
}
}更多【算法-数据结构·排序】相关视频教程:www.yxfzedu.com
相关文章推荐
- 华为-漏刻有时百度地图API实战开发(1)华为手机无法使用addEventListener click 的兼容解决方案 - 其他
- 架构-LoRaWAN物联网架构 - 其他
- clickhouse-【总结卡】clickhouse数据库常用高级函数 - 其他
- java-深入理解ClickHouse跳数索引 - 其他
- 小程序-小程序发成绩 - 其他
- 运维-墨者学院 Ruby On Rails漏洞复现第一题(CVE-2018-3760) - 其他
- fpga开发-「Verilog学习笔记」多功能数据处理器 - 其他
- 前端-TypeScript深度剖析:TypeScript 中枚举类型应用场景? - 其他
- java-Failure to find org.apache.maven.plugins:maven-resources- plugin:jar:3.8.1 - 其他
- 机器学习-Azure - 机器学习:使用自动化机器学习训练计算机视觉模型的数据架构 - 其他
- 网络-网络运维Day01 - 其他
- 机器学习-Azure 机器学习 - 设置 AutoML 训练时序预测模型 - 其他
- java-10-27 maven概念 - 其他
- java-Maven的总结 - 其他
- 学习-【Azure 架构师学习笔记】-Azure Storage Account(5)- Data Lake layers - 其他
- 人工智能-高校为什么需要大数据挖掘平台? - 其他
- 数码相机-立体相机标定 - 其他
- java-java计算 - 其他
- python-前端面试题 - 其他
- git-IntelliJ IDEA 2023.2.1 (Ultimate Edition) 版本 Git 如何合并多次的本地提交进行 Push - 其他
2):严禁色情、血腥、暴力
3):严禁发布任何形式的广告贴
4):严禁发表关于中国的政治类话题
5):严格遵守中国互联网法律法规
6):有侵权,疑问可发邮件至service@yxfzedu.com
- Android安全- 腾讯游戏安全技术竞赛2023 安卓客户端初赛WriteUp
- 软件逆向-2023南极动物厂高校决赛之决赛附加题
- 软件逆向-XXX-xxxx.sys 句柄相关
- DNF基址-2023年4月20日【心悦获取】
- CTF对抗-DASCTF Apr.2023 X SU战队2023开局之战 reverse&&blockchain writeup
- Android安全-2023腾讯游戏安全竞赛决赛题解(安卓)
- 编程技术-CobaltStrike分析1 - stager 生成流程分析
- 软件逆向- 发点好玩的东西 x 2,但是依旧没源码
- 智能设备-EMBA安装、使用与源代码分析_0
- 加壳脱壳-【新手初试】挑战最简单的脱杀Denuvo DRM加密

