数学建模-数学建模函数插值与拟合

1.脑图

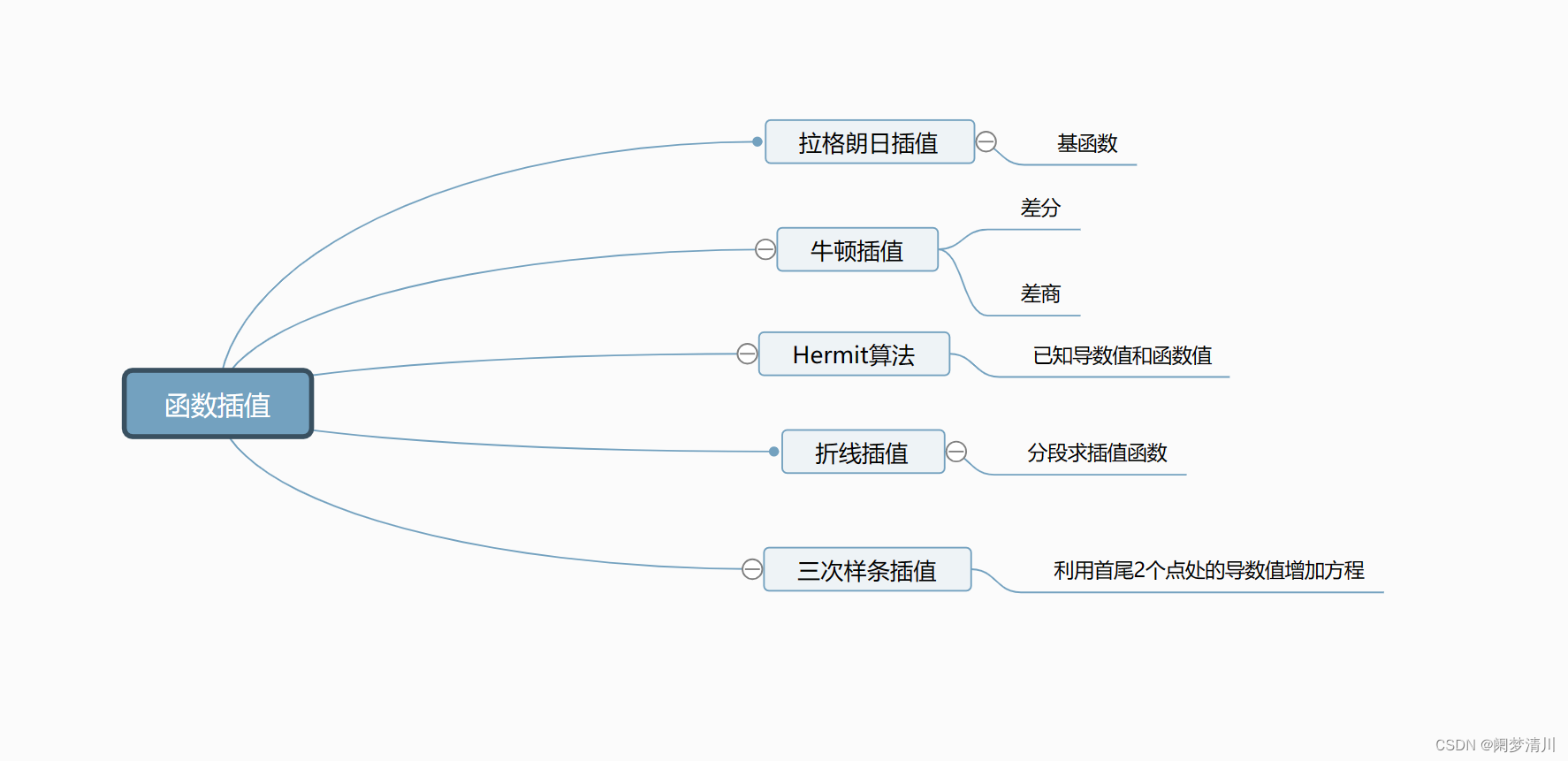
2.介绍

我们自己找到的函数，在已知点处的函数值和要求的函数在这些点处的函数值相等，这个函数

就叫做未知函数的插值函数；

多项式函数构成的插值函数的集合叫做函数类；

3.拉格朗日插值法

基函数的求法和插值函数的构造

这道题目要求的是在0.5处的函数值，我们取的是与之相邻的3个点，这样可以减小误差

3个点处求出的插值多项式叫做二次插值多项式；

就是对应点处的函数值乘上对应的基函数得出插值函数；

但是这种方法的缺陷就是添加几个数据之后就需要重新进行运算；

这个时候我们引入差分和差商的概念；

4.牛顿插值法

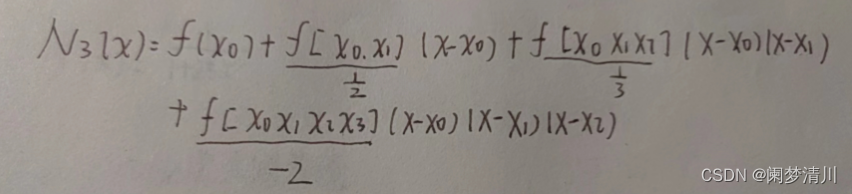
不同的点之间的距离相等时候，也就是等距的情况之下，我们使用差分求插值函数，差分就是两个

点处的函数值做减法；差分和顺序有关系，因为交换位置以后，正数就变成了负数

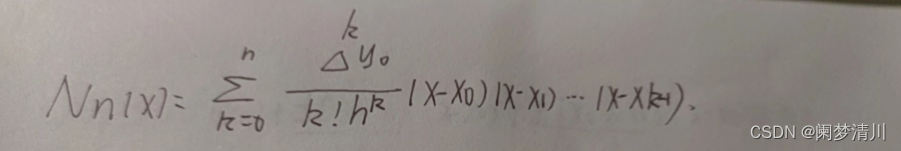
这个时候有了差商，差商就是两个点的函数值的差除以自变量的差，和导数的概念相似；

而且差商和顺序无关，因为如果变号的话，分子分母都会改变，不影响函数值哦；

这里有一阶差商，二阶差商，三阶差商等等，最上面的两张图就是利用差商求插值函数；

牛顿插值法的缺点是随着数据的增加，误差并不是越来越小，因为根据下面的这个误差公式

我们假设分子取最大值，随着数据的变多，n+1的阶乘肯定是变大的，但是分子该点和其他点

的差值的乘积也是变大的，有可能变得比分母还要快，九十的误差变大，因为有很多点离他是

很远的，乘积就会变大；

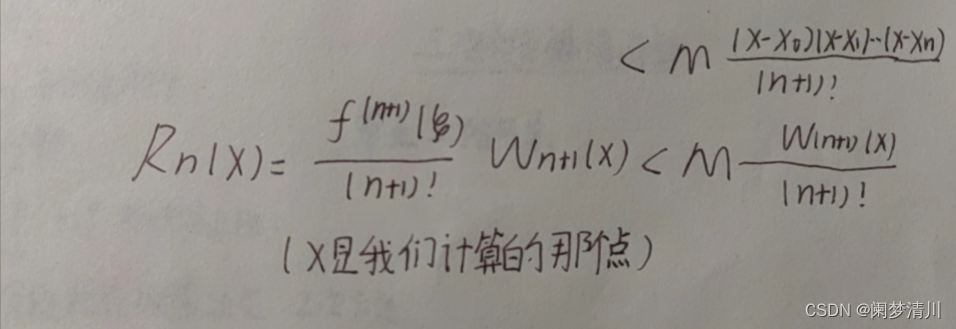
5.低次分段插值

这种就是分段求插值函数，这样就可以提高精度，但是由于在分断点处不可导，所以使得这种解法

不具有和好的分析性质我们不再进行讨论

6.Hermit算法

这种就是一直导数值和函数值，进行求解插值函数，在生活中，设计汽车，流线型很重要，要运用

空气动力学和流体力学的相关知识，这个时候各个点的导数肯定是已经知道的，这个就符合该算法

7.三次样条插值

这种在工程上面的应用比较普遍，给出4个点，求三次样条插值函数，只能列出2个方程这个就要

根据起始点和终点处的导数再次构造出来2个方程进行求解，

函数的差值很小，但是这2个函数的导数的差不一定很小

但是这2个函数的积分差值会足够小。